
【题目】已知函数![]() .
.
(1)若![]() ,求函数
,求函数![]() 的极值和单调区间;
的极值和单调区间;
(2)若在区间![]() 上至少存在一点
上至少存在一点![]() ,使得
,使得![]() 成立,求实数
成立,求实数![]() 的取值范围.
的取值范围.
【答案】(1)极小值是![]() ,
,![]() 的单调递增区间为
的单调递增区间为![]() ,单调递减区间为
,单调递减区间为![]() ;(2)
;(2)![]() .
.
【解析】
试题分析:(1)借助题设条件运用导数求解;(2)先借助导数分类讨论求出最值,再建立不等式求解.
试题解析:
(1)当![]() ,
,
令![]() ,得
,得![]() ,
,
又![]() 的定义域为
的定义域为![]() ,由
,由![]() 得
得![]() ,由
,由![]() ,得
,得![]() ,
,
所以![]() 时,
时,![]() 有极小值为1,
有极小值为1,
![]() 的单调递增区间为
的单调递增区间为![]() ,单调递减区间为
,单调递减区间为![]() .
.
(2)![]() ,且
,且![]() ,令
,令![]() ,得到
,得到![]() ,若在区间
,若在区间![]() 上存在一点
上存在一点![]() ,使得
,使得![]() 成立,即
成立,即![]() 在区间
在区间![]() 上的最小值小于0.
上的最小值小于0.
当![]() ,即
,即![]() 时,
时,![]() 恒成立,即
恒成立,即![]() 在区间
在区间![]() 上单调递减,
上单调递减,
故![]() 在区间
在区间![]() 上的最小值为
上的最小值为![]() ,
,
由![]() ,得
,得![]() ,即
,即![]() .
.
当![]() ,即
,即![]() 时,
时,
①若![]() ,则
,则![]() 对
对![]() 成立,所以
成立,所以![]() 在区间
在区间![]() 上单调递减,
上单调递减,
则![]() 在区间
在区间![]() 上的最小值为
上的最小值为![]() ,
,
显然,![]() 在区间
在区间![]() 上的最小值小于0不成立,
上的最小值小于0不成立,
②若![]() ,即
,即![]() 时,则有
时,则有
|
|
|
|
|
| 0 |
|
|
| 极小值 |
|
所以![]() 在区间
在区间![]() 上的最小值为
上的最小值为![]() ,
,
由![]() ,得
,得![]() ,解得
,解得![]() ,即
,即![]() ,
,
综上,由①②可知:![]() 符合题意.
符合题意.


 高中必刷题系列答案
高中必刷题系列答案科目:高中数学 来源: 题型:
【题目】铁矿石A和B的含铁率为![]() ,冶炼每万吨铁矿石CO2的排放量b及每万吨铁矿石
,冶炼每万吨铁矿石CO2的排放量b及每万吨铁矿石
的价格c如下表:
| b(万吨) |
| |
A | 50% | 1 | 3 |
B | 70% | 0.5 | 6 |
某冶炼厂至少要生产1.9(万吨)铁,若要求CO2的排放量不超过2(万吨),则购买铁矿石的最少费用为________ (百万元).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆C: ![]() ,直线l:
,直线l: ![]()

(Ⅰ)求直线l所过定点A的坐标;
(Ⅱ)求直线l被圆C所截得的弦长最短时m的值及最短弦长;
(Ⅲ)已知点![]() ,在直线MC上(C为圆心),存在定点N(异于点M),满足:对于圆C上任一点P,都有
,在直线MC上(C为圆心),存在定点N(异于点M),满足:对于圆C上任一点P,都有![]() 为一常数,试求所有满足条件的点N的坐标及该常数。
为一常数,试求所有满足条件的点N的坐标及该常数。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某届奥运会上,中国队以26金18银26铜的成绩称金牌榜第三、奖牌榜第二,某校体育爱好者在高三 年级一班至六班进行了“本届奥运会中国队表现”的满意度调查(结果只有“满意”和“不满意”两种),从被调查的学生中随机抽取了50人,具体的调查结果如下表:

(1)在高三年级全体学生中随机抽取一名学生,由以上统计数据估计该生持满意态度的概率;
(2)若从一班至二班的调查对象中随机选取4人进行追踪调查,记选中的4人中对“本届奥运会中国队表现”不满意的人数为![]() ,求随机变量
,求随机变量![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,某企业的两座建筑物AB,CD的高度分别为20m和40m,其底部BD之间距离为20m.为响应创建文明城市号召,进行亮化改造,现欲在建筑物AB的顶部A处安装一投影设备,投影到建筑物CD上形成投影幕墙,既达到亮化目的又可以进行广告宣传.已知投影设备的投影张角∠EAF为![]() ,投影幕墙的高度EF越小,投影的图像越清晰.设投影光线的上边沿AE与水平线AG所成角为α,幕墙的高度EF为y(m).
,投影幕墙的高度EF越小,投影的图像越清晰.设投影光线的上边沿AE与水平线AG所成角为α,幕墙的高度EF为y(m).
(1)求y关于α的函数关系式![]() ,并求出定义域;
,并求出定义域;
(2)当投影的图像最清晰时,求幕墙EF的高度.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】市场上有一种新型的强力洗衣粉,特点是去污速度快,已知每投放![]() (
(![]() 且
且![]() )个单位的洗衣粉液在一定量水的洗衣机中,它在水中释放的浓度
)个单位的洗衣粉液在一定量水的洗衣机中,它在水中释放的浓度![]() (克/升)随着时间
(克/升)随着时间![]() (分钟)变化的函数关系式近似为
(分钟)变化的函数关系式近似为![]() ,其中
,其中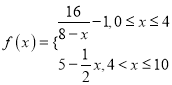 ,若多次投放,则某一时刻水中的洗衣液浓度为每次投放的洗衣液在相应时刻所释放的浓度之和,根据经验,当水中洗衣液的浓度不低于4(克/升)时,它才能起有效去污的作用.
,若多次投放,则某一时刻水中的洗衣液浓度为每次投放的洗衣液在相应时刻所释放的浓度之和,根据经验,当水中洗衣液的浓度不低于4(克/升)时,它才能起有效去污的作用.
(1)若只投放一次4个单位的洗衣液,则有效去污时间可能达几分钟?
(2)若先投放2个单位的洗衣液,6分钟后投放![]() 个单位的洗衣液,要使接下来的4分钟中能够持续有效去污,试求
个单位的洗衣液,要使接下来的4分钟中能够持续有效去污,试求![]() 的最小值(精确到0.1,参考数据:
的最小值(精确到0.1,参考数据: ![]() 取
取![]() ).
).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com