
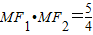 ,
,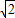 m+1,MF2=
m+1,MF2=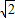 m-1,结合
m-1,结合 求得m的值,从而得出MF1+MF2=3=定值,最后由椭圆的定义得出结论即可;
求得m的值,从而得出MF1+MF2=3=定值,最后由椭圆的定义得出结论即可;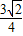 ,
,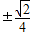 )代入抛物线方程y2=2px(p>0)得焦参数,最后写出抛物线方程.
)代入抛物线方程y2=2px(p>0)得焦参数,最后写出抛物线方程.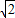 m+1,MF2=
m+1,MF2=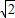 m-1,
m-1,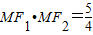
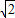 m+1)(
m+1)(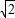 m-1)=
m-1)= ,⇒m=
,⇒m=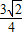
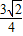 ,
,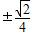 )
)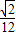
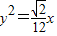 .
.

 英才计划期末调研系列答案
英才计划期末调研系列答案科目:高中数学 来源: 题型:
 如图过抛物线y2=2px(p>0)的焦点F的直线依次交抛物线及准线于点A,B,C,若|BC|=2|BF|,且|AF|=3,则抛物线的方程为( )
如图过抛物线y2=2px(p>0)的焦点F的直线依次交抛物线及准线于点A,B,C,若|BC|=2|BF|,且|AF|=3,则抛物线的方程为( )A、y2=
| ||
| B、y2=9x | ||
C、y2=
| ||
| D、y2=3x |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com