
 ,∴
,∴ ,解之得
,解之得
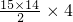 =450台.…(6分)
=450台.…(6分)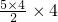 +10×16+
+10×16+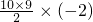 =120<414,
=120<414, ]+[(15-n)(4n-4)+
]+[(15-n)(4n-4)+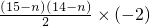 ]=-3n2+93n-270
]=-3n2+93n-270

科目:高中数学 来源: 题型:解答题
 垂直
垂直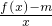 在(0,2)上是减函数,求实数m的取值范围.
在(0,2)上是减函数,求实数m的取值范围.查看答案和解析>>
科目:高中数学 来源: 题型:单选题
| 模块 | 模块选择的学生人数 | 模块 | 模块选择的学生人数 |
| A | 28 | A与B | 11 |
| B | 26 | A与C | 12 |
| C | 26 | B与C | 13 |
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 ,则x的范围是 ________.
,则x的范围是 ________.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
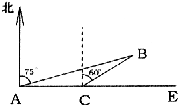 如图,海中有一小岛,周围3.8海里内有暗礁.一军舰从A地出发由西向东航行,望见小岛B在北偏东75°,航行8海里到达C处,望见小岛B在北偏东60°.若此舰不改变舰行的方向继续前进,问此舰有没有触礁的危险?
如图,海中有一小岛,周围3.8海里内有暗礁.一军舰从A地出发由西向东航行,望见小岛B在北偏东75°,航行8海里到达C处,望见小岛B在北偏东60°.若此舰不改变舰行的方向继续前进,问此舰有没有触礁的危险?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com