练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    16．已知直线l的参数方程为$\left\{\begin{array}{l}{x=\frac{1}{2}+\frac{\sqrt{2}}{2}t}\\{y=1+\frac{1}{2}t}\end{array}\right.$（t为参数），圆O的极坐标方程为ρ=$\sqrt{2}$cos（θ-$\frac{π}{4}$）．
    （Ⅰ）将直线l与圆O的方程化为直角坐标方程，并证明直线l过定点P（$\frac{1}{2}$，1）；
    （Ⅱ）设直线l与圆O相交于A、B两点，求证：点P到A、B两点的距离之积为定值．

    分析 （I）直线l的参数方程为$\left\{\begin{array}{l}{x=\frac{1}{2}+\frac{\sqrt{2}}{2}t}\\{y=1+\frac{1}{2}t}\end{array}\right.$（t为参数），消去参数t可得普通方程，即可证明经过定点；圆O的极坐标方程为ρ=$\sqrt{2}$cos（θ-$\frac{π}{4}$），展开可得：${ρ}^{2}=\sqrt{2}×\frac{\sqrt{2}}{2}$（ρcosθ+ρsinθ），利用$\left\{\begin{array}{l}{x=ρcosθ}\\{y=ρsinθ}\end{array}\right.$及其ρ2=x2+y2即可得出直角坐标方程．
    （II）把直线l的标准参数方程$\left\{\begin{array}{l}{x=\frac{1}{2}+\frac{2}{\sqrt{6}}t}\\{y=1+\frac{\sqrt{2}}{\sqrt{6}}t}\end{array}\right.$代入⊙O的方程：x2+y2=x+y，化为：${t}^{2}+\frac{\sqrt{3}}{3}$t-$\frac{1}{4}$=0，可得t1t2=-$\frac{1}{4}$．利用|PA||PB|=|t1t2|即可得出．

    解答 （I）解：直线l的参数方程为$\left\{\begin{array}{l}{x=\frac{1}{2}+\frac{\sqrt{2}}{2}t}\\{y=1+\frac{1}{2}t}\end{array}\right.$（t为参数），消去参数t可得：$x-\frac{1}{2}$=$\sqrt{2}$（y-1），可知直线l过定点P（$\frac{1}{2}$，1），化为一般式：$2x-2\sqrt{2}y$+2$\sqrt{2}$-1=0；
    圆O的极坐标方程为ρ=$\sqrt{2}$cos（θ-$\frac{π}{4}$），展开可得：${ρ}^{2}=\sqrt{2}×\frac{\sqrt{2}}{2}$（ρcosθ+ρsinθ），化为：x2+y2=x+y．
    （II）证明：把直线l的标准参数方程$\left\{\begin{array}{l}{x=\frac{1}{2}+\frac{2}{\sqrt{6}}t}\\{y=1+\frac{\sqrt{2}}{\sqrt{6}}t}\end{array}\right.$代入⊙O的方程：x2+y2=x+y，化为：${t}^{2}+\frac{\sqrt{3}}{3}$t-$\frac{1}{4}$=0，
    ∴t1t2=-$\frac{1}{4}$．
    ∴|PA||PB|=|t1t2|=$\frac{1}{4}$．

    点评 本题考查了极坐标化为直角坐标方程的方法、直线参数方程的应用、圆的方程，考查了推理能力与计算能力，属于中档题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

    6．等比数列{an}中，公比q=2，则$\frac{{a}_{2}+{a}_{4}+{a}_{10}}{{a}_{1}+{a}_{3}+{a}_{9}}$=2．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    7．设函数f（x）=px-$\frac{p}{x}$-2lnx．
    （Ⅰ）若p=1，函数y=f（x）是否有极值，若有，请求出极值，若没有，请说明理由．
    （Ⅱ）若f（x）在其定义域内为单调函数，求实数p的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    4．cosα=$\frac{2}{3}$，α是第四象限角，则sinα=-$\frac{\sqrt{5}}{3}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    11．在实数范围内分解因式x2-6x+8=（x-2）（x-4）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

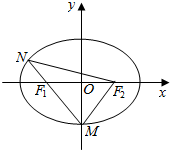    1．如图，已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0），F1、F2分别为椭圆的左、右焦点，M为椭圆的下顶点，直线MF1交椭圆与另一点N．
    （1）若△MF2N的周长为16，${S}_{{{△MF}_{1}F}_{2}}$：${S}_{{△{NF}_{1}F}_{2}}$=3：1，求椭圆的标准方程；
    （2）过点（3，0）且不垂直于坐标轴的直线与椭圆交于A、B两点，已知点C（t，0），当t∈（0，1）时，求满足|AC|=|BC|的直线AB的斜率k的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    8．已知三棱锥V-ABC的底面ABC是边长为4的正三角形，侧棱长都相等，其外接球（三棱锥的每个顶点都在球面上）的球心为O，满足$\overrightarrow{OA}$+$\overrightarrow{OB}$+$\overrightarrow{OC}$=$\overrightarrow{VO}$，则球O的体积为8$\sqrt{6}$π．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    5．由直线x+y+2=0，x+2y+1=0，2x+y+1=0围成的三角形区域（包括边界）用不等式（组）可表示为$\left\{\begin{array}{l}{x+y+2≥0}\\{x+2y+1≤0}\\{2x+y+1≤0}\end{array}\right.$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    6．已知关于x的不等式（1+a）x＞1的解集为{x|x＜$\frac{1}{1+a}$}，试求a的取值范围．

    查看答案和解析>>

    同步练习册答案