设a为实数,函数f(x)=2x2+(x-a)|x-a|
(1)若f(0)≥1,求a的取值范围;
(2)求f(x)的最小值.
分析:(1)不等式即-a|-a|≥1,故有 a<0,且a2≥1,解不等式组求a的取值范围.
(2)分类讨论,去掉绝对值,转化为二次函数的最小值问题,借助二次函数的对称轴及单调性.
解答:解:(1)若f(0)≥1,则:
-a|-a|≥1??a≤-1.
(2)当x≥a时,f(x)=3x
2-2ax+a
2,∴
f(x)min==,如图所示:
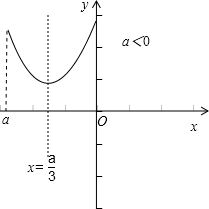
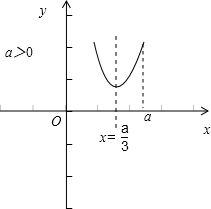
当x≤a时,f(x)=x
2+2ax-a
2,∴
f(x)min==.
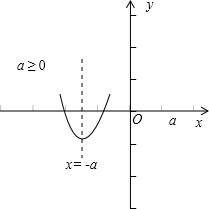
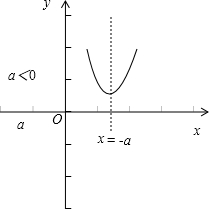
综上所述:
f(x)min=.
点评:本题考查取绝对值的方法,二次函数在区间上的最小值的求法,体现了分类讨论、数形结合的数学思想.






