练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

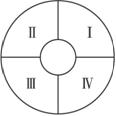
     中央电视台“正大综艺”节目的现场观众来自四个单位,分别在图中4个区域内坐定.有4种不同颜色的服装,每个单位的观众必须穿同种颜色的服装,且相邻两个区域的颜色不同,不相邻区域颜色相同与否则不受限制,那么不同的着装方法有多少种?

    解法一：若每个区域服装颜色不相同,则有C14·C13·C12·1=24种;若Ⅰ、Ⅲ或Ⅱ、Ⅳ同色,另两区域不同色,则有2C14×3×2=48种;若Ⅰ、Ⅲ与Ⅱ、Ⅳ分别同色,则有C24·A22=12种.故共有24+48+12=84种.

    解法二:Ⅰ有4种可能,Ⅱ有3种可能,Ⅲ可与Ⅰ相同或不同,故共有4×3×3+4×3×2×2=84种方法.


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：2013届湖南省高二上学期第一次阶段性考试理科数学试卷 题型：填空题

    中央电视台“正大综艺”节目的现场观众来自4个单位，分别在图中4个区域内坐定。有4种不同的颜色的服装，每个区域的观众必须穿同种颜色的服装，且相邻两个区域的颜色不同，不相邻区域颜色相同与否不受限制，那么不同的着色方法共有____________种。

     

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    8.中央电视台“正大综艺”节目的现场观众来自四个单位，分别在图中4个区域内坐定，有4种不同颜色的服装，每个单位的观众必须穿同种颜色的服装，且相邻两个区域的颜色不

    查看答案和解析>>

    同步练习册答案