
点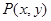 是曲线
是曲线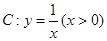 上的动点,曲线
上的动点,曲线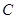 在点
在点 处的切线与
处的切线与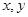 轴分别交于
轴分别交于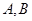 两点,点
两点,点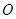 是坐标原点.给出三个结论:①
是坐标原点.给出三个结论:①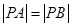 ;②△
;②△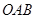 的周长有最小值
的周长有最小值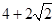 ;③曲线
;③曲线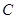 上存在两点
上存在两点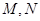 ,使得△
,使得△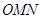 为等腰直角三角形.其中正确结论的个数是
为等腰直角三角形.其中正确结论的个数是
A.1 B.2 C.3 D.0
C
【解析】
试题分析:设动点P(m, )(m>0),则y′=-
)(m>0),则y′=- ,∴f′(m)=-
,∴f′(m)=- ,
,
∴过动点P(m, )的切线方程为:y-
)的切线方程为:y- =-
=- (x-m).
(x-m).
①分别令y=0,x=0,得A(2m,0),B(0, ).
).
则|PA|= ,|PB|=
,|PB|= ,∴|PA|=|PB|,故①正确;
,∴|PA|=|PB|,故①正确;
②由上面可知:△OAB的周长=2m+ +2
+2 ≥2×2+2
≥2×2+2 =4+2
=4+2 ,当且仅当m=
,当且仅当m= ,即m=1时取等号.故△OAB的周长有最小值4+2
,即m=1时取等号.故△OAB的周长有最小值4+2 ,即②正确.
,即②正确.
③假设曲线C上存在两点M(a, ),N(b,
),N(b, ),不妨设0<a<b,∠OMN=90°.
),不妨设0<a<b,∠OMN=90°.
则|ON|= |OM|,
|OM|, ,
,
所以
化为 ,解得
,解得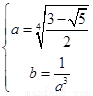 ,故假设成立.因此③正确.
,故假设成立.因此③正确.
故选C。
考点:本题主要考查导数的概念及应用;不等式的解法及应用。
点评:理解导数的几何意义、基本不等式的性质、两点间的距离公式及等腰直角三角形的性质是解题的关键.较难。


科目:高中数学 来源: 题型:
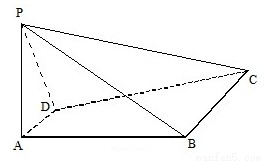
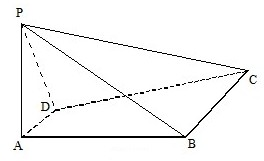 如图,四棱锥P-ABCD中,PA⊥平面ABCD,四边形ABCD是直角梯形,其中DA⊥AB,AD∥BC.PA=2AD=BC=2AB=2
如图,四棱锥P-ABCD中,PA⊥平面ABCD,四边形ABCD是直角梯形,其中DA⊥AB,AD∥BC.PA=2AD=BC=2AB=2| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
(08年龙岩一中冲刺文)(分)已知双曲线C的中心在原点,焦点在x轴上,右准线为![]() 一条渐近线的方程是
一条渐近线的方程是![]() 过双曲线C的右焦点F2的一条弦交双曲线右支于P、Q两点,R是弦PQ的中点.
过双曲线C的右焦点F2的一条弦交双曲线右支于P、Q两点,R是弦PQ的中点.
(1)求双曲线C的方程;
(2)若A、B分别是双曲C上两条渐近线上的动点,且2|AB|=![]() |F1F2|,求线段AB的中点M的迹方程,并说明该轨迹是什么曲线。
|F1F2|,求线段AB的中点M的迹方程,并说明该轨迹是什么曲线。
(3)若在双曲线右准线L的左侧能作出直线m:x=a,使点R在直线m上的射影S满足![]() ,当点P在曲线C上运动时,求a的取值范围.
,当点P在曲线C上运动时,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源:2012-2013学年福建省高三5月月考文科数学试卷(解析版) 题型:解答题
平面内动点 到点
到点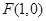 的距离等于它到直线
的距离等于它到直线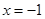 的距离,记点
的距离,记点 的轨迹为曲
的轨迹为曲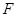 .
.
(Ⅰ)求曲线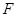 的方程;
的方程;
(Ⅱ)若点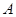 ,
,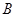 ,
, 是
是 上的不同三点,且满足
上的不同三点,且满足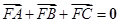 .证明:
.证明: 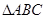 不可能为直角三角形.
不可能为直角三角形.
查看答案和解析>>
科目:高中数学 来源:2009年上海市普陀区高考数学二模试卷(理科)(解析版) 题型:解答题
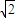 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com