
 已知离心率为
已知离心率为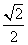 的椭圆
的椭圆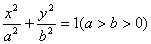 的右焦点
的右焦点 是圆
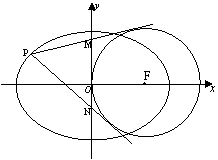
是圆 的圆心,过椭圆上的动点P作圆的两条切线分别交
的圆心,过椭圆上的动点P作圆的两条切线分别交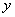 轴于M、N两点.
轴于M、N两点.
(I)求椭圆的方程;
(II)求线段MN长的最大值,并求此时点P的坐标.
本题主要考查直线、圆、椭圆等基础知识,考查函数与方程思想、分类与整合思想、及化归与转化思想.满分14分.
解:(I)∵圆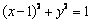 的圆心是
的圆心是 ,
,
∴椭圆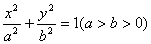 的右焦点 F
的右焦点 F ,……………………1分
,……………………1分
∵椭圆的离心率是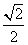 ,∴
,∴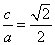
∴ ,∴椭圆的方程是
,∴椭圆的方程是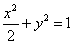 .……………………4分
.……………………4分
(II)解法一:设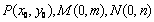 ,
,
由 得
得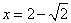 ,∴
,∴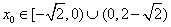 .…………5分
.…………5分
直线 的方程:
的方程: ,
,
化简得 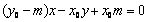 .
.
又圆心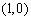 到直线
到直线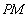 的距离为1,∴
的距离为1,∴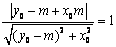 ,………………6分
,………………6分
∴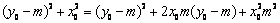 ,
,
化简得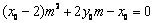 ,
………………………………………………7分
,
………………………………………………7分
同理有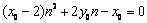 .
……………………………………………… 8分
.
……………………………………………… 8分
∴ ,
, ,……………………………………………………9分
,……………………………………………………9分
∴
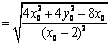 .………………………………10分
.………………………………10分
∵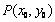 是椭圆上的点,∴
是椭圆上的点,∴ ,
,
∴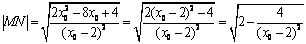 ,……………………11分
,……………………11分
记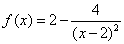 ,则
,则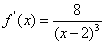 ,
,
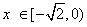 时,
时,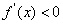 ;
;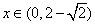 时,
时,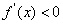 ,
,
∴ 在
在 上单调递减,在
上单调递减,在 内也是单调递减,………………13分
内也是单调递减,………………13分
∴ ,
,
当 时,
时,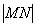 取得最大值
取得最大值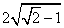 ,
,
此时点P位置是椭圆的左顶点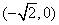 . …………………………14分
. …………………………14分
解法二:由 得
得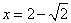 ,∴
,∴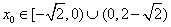 .……5分
.……5分
设过点P的圆的切线方程为 ,
,
∵圆心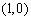 到直线
到直线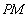 的距离为1,
的距离为1,
∴
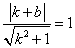 ,化简得
,化简得 ,∴
,∴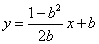 .…………6分
.…………6分
设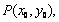 则
则 ,…………………………8分
,…………………………8分
∴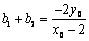 ,
,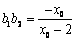 ,……………………………………9分
,……………………………………9分
∴
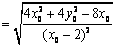 .…………………10分
.…………………10分
∵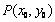 是椭圆上的点,∴
是椭圆上的点,∴ ,
,
∴ ,………………11分
,………………11分
记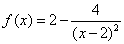 ,则
,则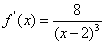 ,
,
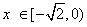 时,
时,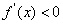 ;
;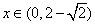 时,
时,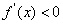 ,
,
∴ 在
在 上单调递减,在
上单调递减,在 内也是单调递减,…………13分
内也是单调递减,…………13分
∴ ,
,
当 时,
时,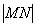 取得最大值
取得最大值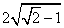 ,
,
此时点P位置是椭圆的左顶点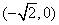 . ………………………………14分
. ………………………………14分


 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案科目:高中数学 来源: 题型:
 . 已知离心率为
. 已知离心率为![]() 的椭圆
的椭圆![]() 的右焦点
的右焦点![]() 是圆
是圆![]() 的圆心,过椭圆上的动点P作圆的两条切线分别交
的圆心,过椭圆上的动点P作圆的两条切线分别交![]() 轴于M、N两点.
轴于M、N两点.
(I)求椭圆的方程;
(II)求线段MN长的最大值,并求此时点P的坐标.
查看答案和解析>>
科目:高中数学 来源:2011-2012学年广西桂林十八中高三第二次月考试卷理科数学 题型:解答题
(本小题满分12分)已知离心率为 的椭圆
的椭圆 上的点到
上的点到
左焦点 的最长距离为
的最长距离为
(1)求椭圆的方程;
(2)如图,过椭圆的左焦点 任作一条与两坐标轴都不垂直的弦
任作一条与两坐标轴都不垂直的弦 ,若点
,若点 在
在 轴上,且使得
轴上,且使得 为
为 的一条内角平分线,则称点
的一条内角平分线,则称点 为该椭圆的“左特征点”,求椭圆的“左特征点”
为该椭圆的“左特征点”,求椭圆的“左特征点” 的坐标.
的坐标.

查看答案和解析>>
科目:高中数学 来源:2012年广东省华南师大附中高三周六自测数学试卷1(文科)(解析版) 题型:解答题
 的椭圆C的中心在坐标原点O,一焦点坐标为(1,0),圆O的方程为x2+y2=7.
的椭圆C的中心在坐标原点O,一焦点坐标为(1,0),圆O的方程为x2+y2=7.
查看答案和解析>>
科目:高中数学 来源:2010年福建省厦门市高三质量检查数学试卷(理科)(解析版) 题型:解答题
 的椭圆
的椭圆 的右焦点F是圆(x-1)2+y2=1的圆心,过椭圆上的动点P作圆的两条切线分别交y轴于M、N两点.
的右焦点F是圆(x-1)2+y2=1的圆心,过椭圆上的动点P作圆的两条切线分别交y轴于M、N两点.
查看答案和解析>>
科目:高中数学 来源:广西桂林十八中2011-2012学年高三第二次月考试题数学理 题型:解答题
已知离心率为 的椭圆
的椭圆 上的点到左焦点
上的点到左焦点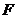 的最长距离为
的最长距离为
(1)求椭圆的方程;
(2)如图,过椭圆的左焦点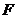 任作一条与两坐标轴都不垂直的弦
任作一条与两坐标轴都不垂直的弦 ,若点
,若点 在
在 轴上,且使得
轴上,且使得 为
为 的一条内角平分线,则称点
的一条内角平分线,则称点 为该椭圆的“左特征点”,求椭圆的“左特征点”
为该椭圆的“左特征点”,求椭圆的“左特征点” 的坐标.
的坐标.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com