解(1)∵e=

.又2c=2,解得a=

,
则b=
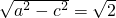
.
(2)
由
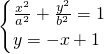
消去y得(a
2+b
2)•x
2-2a
2x+a
2•(1-b
2)=0,
由△=(-2a
2)
2-4a
2(a
2+b
2)(1-b
2)>0,整理得a
2+b
2>1.
设A(x
1,y
1,),B(x
2,y
2),
则x
1+x
2=

.
∴y
1y
2=(-x
1+1)(-x
2+1)=x
1x
2-(x
1+x
2)+1.
∵OA⊥OB(其中O为坐标原点),
∴x
1x
2+y
1y
2=0,即2x
1x
2-(x
1+x
2)+1=0.
∴

+1=0.整理得a
2+b
2-2a
2b
2=0.
∵b
2=a
2-c
2=a
2-a
2e
2,代入上式得
2a
2=1+
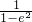
,
∴a
2=
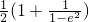
.
∵e∈
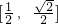
∴
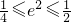
,
∴

,
∴
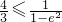
≤2,∴
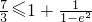
≤3,
∴
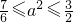
,适合条件a
2+b
2>1,
由此得
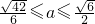
.
∴
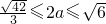
,
故长轴长的最大值为

分析:(1)利用椭圆的离心率公式求出椭圆中的参数a,利用椭圆中三个参数的关系求出b,代入椭圆的方程求出椭圆的标准方程.
(2)将直线的方程与椭圆的方程联立,利用韦达定理求出两个交点的横、纵坐标之积;利用向量垂直的充要条件将
OA⊥OB用交点的坐标表示,得到椭圆的三个参数的一个等式,再利用椭圆的三个参数本身的关系得到参数a与离心率的关系,利用离心率的范围求出a的范围,得到椭圆的长轴长的最大值.
点评:求圆锥曲线的方程,一般利用待定系数法;解决直线与圆锥曲线的位置关系问题,一般设出直线方程,将直线方程与圆锥曲线方程联立,消去一个未知数,得到关于一个未知数的二次方程,利用韦达定理,找突破口.注意设直线方程时,一定要讨论直线的斜率是否存在.

 =1(a>b>0)相交于A、B两点.
=1(a>b>0)相交于A、B两点. ,焦距为2,求椭圆的标准方程;
,焦距为2,求椭圆的标准方程;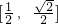 时,求椭圆的长轴长的最大值.
时,求椭圆的长轴长的最大值. .又2c=2,解得a=
.又2c=2,解得a= ,
,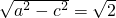 .
.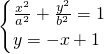
 .
. +1=0.整理得a2+b2-2a2b2=0.
+1=0.整理得a2+b2-2a2b2=0.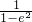 ,
,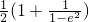 .
.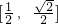 ∴
∴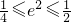 ,
, ,
,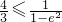 ≤2,∴
≤2,∴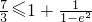 ≤3,
≤3,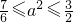 ,适合条件a2+b2>1,
,适合条件a2+b2>1,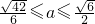 .
.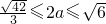 ,
,

