
佛山某中学高三(1)班排球队和篮球队各有 名同学,现测得排球队
名同学,现测得排球队 人的身高(单位:
人的身高(单位: )分别是:
)分别是: 、
、 、
、 、
、 、
、 、
、 、
、 、
、 、
、 、
、 ,篮球队
,篮球队 人的身高(单位:
人的身高(单位: )分别是:
)分别是: 、
、 、
、 、
、 、
、 、
、 、
、 、
、 、
、 、
、 .
.
(Ⅰ)请把两队身高数据记录在如图所示的茎叶图中,并指出哪个队的身高数据方差较小(无需计算);
(Ⅱ)现从两队所有身高超过
 的同学中随机抽取三名同学,则恰好两人来自排球队一人来自篮球队的概率是多少?
的同学中随机抽取三名同学,则恰好两人来自排球队一人来自篮球队的概率是多少?
(Ⅰ) 篮球队的身高数据方差较小;(Ⅱ) .
.
解析试题分析:(Ⅰ)用中间的数字表示百位数和十位数,两边的数字表示个位数,茎按从小到大的顺序(或从大到小的顺序)从上向下列出,共茎的叶一般按从大到小(或从小到大)的顺序同行列出,从茎叶图中可以看出篮球队身高数字较为集中,故方差较小;(Ⅱ) 两队所有身高超过
 的同学恰有
的同学恰有 人,其中
人,其中 人来自排球队,
人来自排球队, 人来自篮球队,分别编号,并列出从
人来自篮球队,分别编号,并列出从 人中抽取
人中抽取 名同学的基本事件总数,以及恰好两人来自排球队、一人来自篮球队包含的基本事件数,代入古典型的概率计算公式即可.
名同学的基本事件总数,以及恰好两人来自排球队、一人来自篮球队包含的基本事件数,代入古典型的概率计算公式即可.
试题解析:(Ⅰ)茎叶图如图所示,篮球队的身高数据方差较小.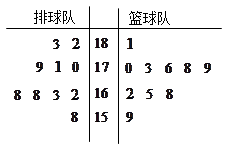
(Ⅱ) 两队所有身高超过
 的同学恰有
的同学恰有 人,其中
人,其中 人来自排球队,记为
人来自排球队,记为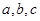 ,
, 人来自篮球队,记为
人来自篮球队,记为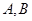 ,则从
,则从 人中抽取
人中抽取 名同学的基本事件为:
名同学的基本事件为: ,
,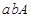 ,
,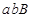 ,
,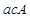 ,
,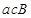 ,
,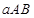 ,
, ,
,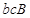 ,
, ,
,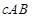 共
共 个;其中恰好两人来自排球队一人来自篮球队所含的事件有:
个;其中恰好两人来自排球队一人来自篮球队所含的事件有: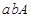 ,
,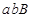 ,
,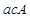 ,
,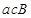 ,
, ,
,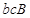 共
共 个, 所以,恰好两人来自排球队一人来自篮球队的概率是
个, 所以,恰好两人来自排球队一人来自篮球队的概率是 .
.
考点:1、茎叶图;2、方差;3、古典概型.


科目:高中数学 来源: 题型:解答题
若某产品的直径长与标准值的差的绝对值不超过1mm时,则视为合格品,否则视为不合格品.在近期一次产品抽样检查中,从某厂生产的此种产品中,随机抽取5000件进行检测,结果发现有50件不合格品.计算这50件不合格品的直径长与标准值的差(单位:mm),将所得数据分组,得到如下频率分布表:
| 分 组 | 频 数 | 频 率 |
| [-3,-2) | | 0.10 |
| [-2,-1) | 8 | |
| (1,2] | | 0.50 |
| (2,3] | 10 | |
| (3,4] | | |
| 合计 | 50 | 1.00 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
对甲、乙两名自行车赛手在相同条件下进行了6次测试,测得他们的最大速度(m/s)的数据如下表.
| 甲 | 27 | 38 | 30 | 37 | 35 | 31 |
| 乙 | 33 | 29 | 38 | 34 | 28 | 36 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
据《中国新闻网》10月21日报道,全国很多省市将英语考试作为高考改革的重点,一时间“英语考试该如何改”引起广泛关注.为了解某地区学生和包括老师、家长在内的社会人士对高考英语改革的看法,某媒体在该地区选择了3600人调查(若所选择的在校学生的人数低于被调查人群总数的80%,则认为本次调查“失效”),就“是否取消英语听力”的问题,调查统计的结果如下表:
| 应该取消 | 应该保留 | 无所谓 | ||
| 在校学生 | 2100人 | 120人 | y人 | ||
| 社会人士 | 600人 | x人 | z人 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
根据空气质量指数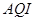 (为整数)的不同,可将空气质量分级如下表:
(为整数)的不同,可将空气质量分级如下表:
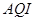 (数值) (数值) |  |  |  |  |  |  |
| 空气质量级别 | 一级 | 二级 | 三级 | 四级 | 五级 | 六级 |
| 空气质量类别 | 优 | 良 | 轻度污染 | 中度污染 | 重度污染 | 严重污染 |
| 空气质量类别颜色 | 绿色 | 黄色 | 橙色 | 红色 | 紫色 | 褐红色 |
 年
年 月
月 日—
日— 月
月 日,对空气质量指数
日,对空气质量指数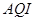 进行监测,获得数据后得到如图的条形图
进行监测,获得数据后得到如图的条形图
 天计)空气质量类别为中度污染的概率;
天计)空气质量类别为中度污染的概率; 个,求至少有一个数据反映的空气质量类别颜色为褐红色的概率.
个,求至少有一个数据反映的空气质量类别颜色为褐红色的概率.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某工厂有25周岁以上(含2S周岁)工人300名,25周岁以下工人200名为研究工人的日平均生产量是否与年龄有关,现采用分层抽样的方法,从中抽取了100名工人,先统计了他们某月的日平均生产件数,然后按工人年龄在“25周岁以上(含25周岁)”和“25周岁以下”分为两组,再将两组工人的日平均生产件数分成5组:[50,60), [60,70), [70,80), [80,90), [90,100), 分别加以统计,得到如图所示的频率分布直方图。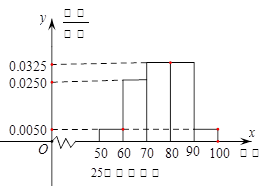
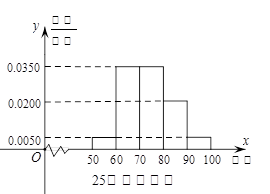
(1)求样本中“25周岁以上(含25周岁)组”抽取的人数、日生产量平均数;
(2)若“25周岁以上组”中日平均生产90件及90件以上的称为“生产能手”;“25周岁以下组”中日平均生产不足60件的称为“菜鸟”。从样本中的“生产能手”和”菜鸟”中任意抽取2人,求这2人日平均生产件数之和X的分布列及期望。(“生产能手”日平均生产件数视为95件,“菜鸟”日平均生产件数视为55件)。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某英语学习小组共12名同学进行英语听力测试,随机抽取6名同学的测试成绩(单位:分),用茎叶图记录如下,其中茎为十位数,叶为个位数.
(1)根据茎叶图计算样本均值;
(2)成绩高于样本均值的同学为优秀,根据茎叶图估计该小组12名同学中有几名优秀同学;
(3)从该小组12名同学中任取2人,求仅有1人是来自随机抽取6人中优秀同学的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
为预防H7N9病毒爆发,某生物技术公司研制出一种新流感疫苗,为测试该疫苗的有效性(若疫苗有效的概率小于90%,则认为测试没有通过),公司选定2000个流感样本分成三组,测试结果如下表:
| 分组 | A组 | B组 | C组 |
| 疫苗有效 | 673 | a | b |
| 疫苗无效 | 77 | 90 | c |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
为了对某课题进行研究,用分层抽样方法从三所科研单位A、B、C的相关人员中,抽取若干人组成研究小组,有关数据见下表(单位:人):
| 科研单位 | 相关人数 | 抽取人数 |
| A | 16 |  |
| B | 12 | 3 |
| C | 8 | 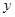 |
 与
与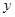 的值;
的值;查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com