
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
分析 直接由复数代数形式的乘除运算化简$\frac{-1+\sqrt{3}i}{1+i}$,再由复数求模公式求出|$\frac{-1+\sqrt{3}i}{1+i}$|,代入已知条件化简求出复数z在复平面内对应的点的坐标,则答案可求.
解答 解:∵$\frac{-1+\sqrt{3}i}{1+i}$=$\frac{(-1+\sqrt{3}i)(1-i)}{(1+i)(1-i)}=\frac{-1+\sqrt{3}+(1+\sqrt{3})i}{2}$=$\frac{-1+\sqrt{3}}{2}+\frac{1+\sqrt{3}}{2}i$,
∴|$\frac{-1+\sqrt{3}i}{1+i}$|=$\sqrt{(\frac{-1+\sqrt{3}}{2})^{2}+(\frac{1+\sqrt{3}}{2})^{2}}=\sqrt{2}$.
由iz=|$\frac{-1+\sqrt{3}i}{1+i}$|+2i=$\sqrt{2}+2i$,
得$z=\frac{\sqrt{2}+2i}{i}$=$\frac{-i(\sqrt{2}+2i)}{-{i}^{2}}=2-\sqrt{2}i$.
则复数z在复平面内所对应的点的坐标为:(2,$-\sqrt{2}$),位于第四象限.
故选:D.
点评 本题考查了复数代数形式的乘除运算,考查了复数的代数表示法及其几何意义,是基础题.


 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案科目:高中数学 来源: 题型:解答题
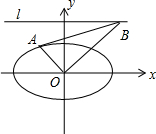 如图,已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右焦点分别为F1,F2,离心率为$\frac{\sqrt{2}}{2}$,点A是椭圆C上任意一点,且△AF1F2的周长为2($\sqrt{2}$+1)
如图,已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右焦点分别为F1,F2,离心率为$\frac{\sqrt{2}}{2}$,点A是椭圆C上任意一点,且△AF1F2的周长为2($\sqrt{2}$+1)查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| x | 3 | 6 | 7 | 9 | 10 |
| y | 12 | 10 | 8 | 8 | 7 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | -$\frac{5}{7}$ | C. | $\frac{5}{7}$ | D. | -1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com