
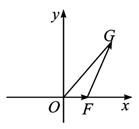
(1)求x0关于t的函数x0=f(t)的表达式,判断函数f(t)的单调性,并证明你的判断;
(2)设△OFG的面积S=![]() t,若以O为中心、F为焦点的椭圆经过点G,求当|
t,若以O为中心、F为焦点的椭圆经过点G,求当|![]() |取得最小值时椭圆的方程.
|取得最小值时椭圆的方程.
解:(1)由题意知![]() =(x0-t,y0),
=(x0-t,y0), ![]() =(t,0),则
=(t,0),则![]() ·
·![]() =t(x0-t)=1.
=t(x0-t)=1.
解得x0=f(t)=t+![]() .
.
设t1>t2≥3,则f(t1)-f(t2)=(t1+![]() )-(t2+
)-(t2+![]() )=(t1-t2)-
)=(t1-t2)-![]() =(t1-t2)
=(t1-t2)![]() .
.
∵t1-t2>0,t1t2-1>0,t1t2>0,
∴f(t1)-f(t2)>0,f(t1)>f(t2),函数f(t)在区间[3,+∞]上单调递增.
(2)由S=![]() |
|![]() ||y0|=
||y0|=![]() ×t×|y0|=
×t×|y0|=![]() t,得y0=±
t,得y0=±![]() .
.
∴点G的坐标为(t+![]() ,±
,±![]() ),|
),|![]() |2=(t+
|2=(t+![]() )2+
)2+![]() .
.
∵函数f(t)在区间[3,+∞]上单调递增,
∴当t=3时,| ![]() |取得最小值,此时点F、G的坐标分别为(3,0)、(
|取得最小值,此时点F、G的坐标分别为(3,0)、(![]() ,±
,±![]() ).
).
由题意设椭圆方程为![]() +
+![]() =1.
=1.
由点G在椭圆上,得![]() +
+![]() =1,
=1,
解得b2=9.
∴所求椭圆方程为![]() +
+![]() =1.
=1.


科目:高中数学 来源: 题型:
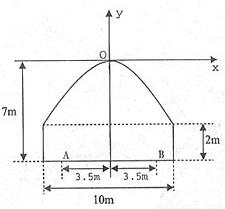
 如图所示,一隧道内设双行线公路,其截面由长方形的三条边和抛物线的一段构成,为保证安全,要求行驶车辆顶部(设为平顶)与隧道顶部在竖直方向上高度之差至少要有0.5米.
如图所示,一隧道内设双行线公路,其截面由长方形的三条边和抛物线的一段构成,为保证安全,要求行驶车辆顶部(设为平顶)与隧道顶部在竖直方向上高度之差至少要有0.5米.查看答案和解析>>
科目:高中数学 来源:2008-2009学年福建省泉州市惠安县惠南中学高二(上)期末数学试卷(选修2-1)(理科)(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com