
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),
为参数),![]() 为
为![]() 上的动点,
上的动点,![]() 点满足
点满足![]() ,点
,点![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(1)求曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)在以为![]() 极点,
极点,![]() 轴的正半轴为极轴的极坐标系中,射线
轴的正半轴为极轴的极坐标系中,射线![]() 与
与![]() 的异于极点的交点为
的异于极点的交点为![]() ,与
,与![]() 的异于极点的交点为
的异于极点的交点为![]() ,求
,求![]() .
.
科目:高中数学 来源: 题型:
【题目】中国古代十进制的算筹计数法,在数学史上是一个伟大的创造.根据史书的记载和考古材料的发现,古代的算筹实际上是一根根同样长短和粗细的小棍子,一般长为![]() ,径粗
,径粗![]() ,多用竹子制成,也有用木头、兽骨、象牙、金属等材料制成的,大约二百七十几枚为一束,放在一个布袋里,系在腰部随身携带.需要记数和计算的时候,就把它们取出来,放在桌上、炕上或地上都能摆弄.在算筹计数法中,以纵横两种排列方式来表示数字.如图,是利用算筹表示数1~9的一种方法.例如:3可表示为“
,多用竹子制成,也有用木头、兽骨、象牙、金属等材料制成的,大约二百七十几枚为一束,放在一个布袋里,系在腰部随身携带.需要记数和计算的时候,就把它们取出来,放在桌上、炕上或地上都能摆弄.在算筹计数法中,以纵横两种排列方式来表示数字.如图,是利用算筹表示数1~9的一种方法.例如:3可表示为“![]() ”,26可表示为“
”,26可表示为“![]() ”,现有6根算筹,据此表示方法,若算筹不能剩余,则用这6根算筹能表示的两位数的个数为( )
”,现有6根算筹,据此表示方法,若算筹不能剩余,则用这6根算筹能表示的两位数的个数为( )
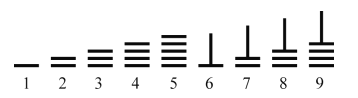
A.13B.14C.15D.16
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2016年1月1日,我国全面实行二孩政策,某机构进行了街头调查,在所有参与调查的青年男女中,持“响应”“犹豫”和“不响应”态度的人数如下表所示:
响应 | 犹豫 | 不响应 | |
男性青年 | 500 | 300 | 200 |
女性青年 | 300 | 200 | 300 |
根据已知条件完成下面的![]() 列联表,并判断能否有
列联表,并判断能否有![]() 的把握认为犹豫与否与性别有关?请说明理由.
的把握认为犹豫与否与性别有关?请说明理由.
犹豫 | 不犹豫 | 总计 | |
男性青年 | |||
女性青年 | |||
总计 | 1800 |
参考公式:![]()
参考数据:
| 0.150 | 0.100 | 0.050 | 0.025 | 0.010 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在打击拐卖儿童犯罪的活动中,警方救获一名男孩,为了确定他的家乡,警方进行了调查:
知情人士A说,他可能是四川人,也可能是贵州人;
知情人士B说,他不可能是四川人;
知情人士C说,他肯定是四川人;
知情人士D说,他不是贵州人.
警方确定,只有一个人的话不可信.根据以上信息,警方可以确定这名男孩的家乡是( )
A.四川B.贵州
C.可能是四川,也可能是贵州D.无法判断
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2018年9月24日,阿贝尔奖和菲尔兹奖双料得主、英国著名数学家阿蒂亚爵士宣布自己证明了黎曼猜想,这一事件引起了数学届的震动。在1859年的时候,德国数学家黎曼向科学院提交了题目为《论小于某值的素数个数》的论文并提出了一个命题,也就是著名的黎曼猜想。在此之前,著名数学家欧拉也曾研究过这个问题,并得到小于数字![]() 的素数个数大约可以表示为
的素数个数大约可以表示为![]() 的结论。若根据欧拉得出的结论,估计1000以内的素数的个数为_________(素数即质数,
的结论。若根据欧拉得出的结论,估计1000以内的素数的个数为_________(素数即质数,![]() ,计算结果取整数)
,计算结果取整数)
A. 768 B. 144 C. 767 D. 145
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知梯形![]() 中,
中,![]() ,
,![]() ,
,![]() ,四边形
,四边形![]() 为矩形,
为矩形,![]() ,平面
,平面![]() 平面
平面![]() .
.

(Ⅰ)求证:![]() 平面
平面![]() ;
;
(Ⅱ)求平面![]() 与平面
与平面![]() 所成锐二面角的余弦值;
所成锐二面角的余弦值;
(Ⅲ)在线段![]() 上是否存在点
上是否存在点![]() ,使得直线
,使得直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() ,若存在,求出线段
,若存在,求出线段![]() 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市委积极响应十九大报告提出的“到2020年全面建成小康社会”的目标,鼓励各县积极脱贫,计划表彰在农村脱贫攻坚战中的杰出村代表,已知A,B两个贫困县各有15名村代表,最终A县有5人表现突出,B县有3人表现突出,现分别从A,B两个县的15人中各选1人,已知有人表现突出,则B县选取的人表现不突出的概率是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C对应的边分别是a,b,c,已知cos2A﹣3cos(B+C)=1.
(1)求角A的大小;
(2)若△ABC的面积S=5![]() ,b=5,求sinBsinC的值.
,b=5,求sinBsinC的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,函数
,函数![]() 的图象在
的图象在![]() 处的切线与直线
处的切线与直线![]() 平行.
平行.
(Ⅰ)求实数![]() 的值;
的值;
(Ⅱ)若函数![]() 存在单调递减区间,求实数
存在单调递减区间,求实数![]() 的取值范围;
的取值范围;
(Ⅲ)设![]() (
(![]() )是函数
)是函数![]() 的两个极值点,若
的两个极值点,若![]() ,试求
,试求![]() 的最小值.
的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com