
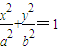 (a>b>0)的右焦点F的直线L与椭圆交于A、B两点,M是线段AB的中点,直线AB与直线OM(O是坐标原点)的斜率分别为k、m,且km=
(a>b>0)的右焦点F的直线L与椭圆交于A、B两点,M是线段AB的中点,直线AB与直线OM(O是坐标原点)的斜率分别为k、m,且km=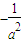 .
.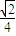 ,连接OM并延长交椭圆于点C,若四边形OACB恰好是平行四边形,求椭圆的方程.
,连接OM并延长交椭圆于点C,若四边形OACB恰好是平行四边形,求椭圆的方程.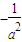 ,即可求b的值;
,即可求b的值; ,从而可求C的坐标,利用C在椭圆上,即可求得椭圆的方程.
,从而可求C的坐标,利用C在椭圆上,即可求得椭圆的方程.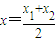 ,m=
,m= ,…(4分)
,…(4分) ,y=k(x-c)=-
,y=k(x-c)=-
 =-
=-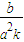 ,∴km=-
,∴km=-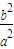 ;
; ,∴b=1; …(6分)
,∴b=1; …(6分)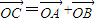 ,…(8分)
,…(8分) =
=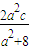 ,yc=y1+y2=2y=
,yc=y1+y2=2y=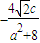 ,
,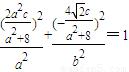 ,…(10分)
,…(10分)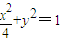 . …(12分)
. …(12分)

科目:高中数学 来源:湖南省模拟题 题型:解答题
 y=0经过椭圆
y=0经过椭圆 (a>b>0)的右焦点F及上顶点B,过椭圆外一点(m,0)(m>a)且倾斜角为
(a>b>0)的右焦点F及上顶点B,过椭圆外一点(m,0)(m>a)且倾斜角为 的直线l交椭圆于C,D两点,
的直线l交椭圆于C,D两点, ,求m的取值范围。
,求m的取值范围。 
查看答案和解析>>
科目:高中数学 来源:2010-2011学年福建省泉州一中高三(上)期末数学试卷(理科)(解析版) 题型:解答题
 如图,已知圆
如图,已知圆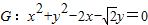 ,经过椭圆
,经过椭圆 (a>b>0)的右焦点F及上顶点B,过椭圆外一点(m,0)(m>a)倾斜角为
(a>b>0)的右焦点F及上顶点B,过椭圆外一点(m,0)(m>a)倾斜角为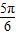 的直线1交椭圆于C,D两点
的直线1交椭圆于C,D两点查看答案和解析>>
科目:高中数学 来源:2010-2011学年安徽省安庆市潜山中学复读班高三(上)周考数学试卷(理科)(9.19)(解析版) 题型:解答题
 如图,已知圆
如图,已知圆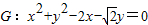 ,经过椭圆
,经过椭圆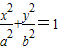 (a>b>0)的右焦点F及上顶点B,过椭圆外一点(m,0)(m>a)倾斜角为
(a>b>0)的右焦点F及上顶点B,过椭圆外一点(m,0)(m>a)倾斜角为 的直线1交椭圆于C,D两点
的直线1交椭圆于C,D两点查看答案和解析>>
科目:高中数学 来源:2012-2013学年河南省郑州一中高三综合测试数学试卷(四)(解析版) 题型:解答题
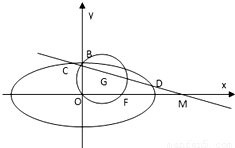 如图,已知圆
如图,已知圆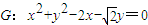 ,经过椭圆
,经过椭圆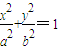 (a>b>0)的右焦点F及上顶点B,过椭圆外一点(m,0)(m>a)倾斜角为
(a>b>0)的右焦点F及上顶点B,过椭圆外一点(m,0)(m>a)倾斜角为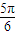 的直线1交椭圆于C,D两点
的直线1交椭圆于C,D两点查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com