
【题目】给定无穷数列![]() ,若无穷数列
,若无穷数列![]() 满足:对任意的
满足:对任意的![]() ,都有
,都有![]() ,则称
,则称![]() 与
与![]() “比较接近”.
“比较接近”.
(1)设![]() 是首项为1,公比为
是首项为1,公比为![]() 的等比数列,
的等比数列,![]() ,判断数列
,判断数列![]() 是否与
是否与![]() “比较接近”;
“比较接近”;
(2)设数列![]() 的前四项为:
的前四项为:![]() ,
,![]() 是一个与
是一个与![]() 比较接近的数列,记集合
比较接近的数列,记集合![]() ,求
,求![]() 中元素的个数
中元素的个数![]() ;
;
(3)已知![]() 是公差为
是公差为![]() 的等差数列,若存在数列
的等差数列,若存在数列![]() 满足:
满足:![]() 与
与![]() 较接近,且在
较接近,且在![]() 中至少有1009个为正,求
中至少有1009个为正,求![]() 的取值范围.
的取值范围.
【答案】(1)接近;
(2)3或4;
(3)![]()
【解析】
(1)运用等比数列的通项公式和新定义“接近”,即可判断;
(2)由新定义可得![]() ,求得
,求得![]() 的范围,即可得到所求
的范围,即可得到所求![]() 中元素的个数;
中元素的个数;
(3)运用等差数列的通项公式可得![]() ,讨论公差的范围,结合新定义“接近”,分别取满足题意的数列
,讨论公差的范围,结合新定义“接近”,分别取满足题意的数列![]() ,再进行推理和运算,即可得到所求的范围.
,再进行推理和运算,即可得到所求的范围.
(1)数列![]() 与
与![]() “比较接近”,理由如下:
“比较接近”,理由如下:
因为![]() 是首项为1,公比为
是首项为1,公比为![]() 的等比数列,所以
的等比数列,所以![]() ,
,
又因为![]() ,所以
,所以![]() ,
,
所以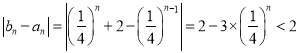 ,
,
所以数列![]() 与
与![]() “比较接近”.
“比较接近”.
(2)因为![]() 是一个与
是一个与![]() 比较接近的数列,所以
比较接近的数列,所以![]() ,即
,即![]() ,
,
因为数列![]() 的前四项为:
的前四项为:![]() ,所以
,所以![]() ,
,![]() ,
,![]() ,
,![]() ,
,
所以在![]() 中
中![]() 与
与![]() 可能相等,
可能相等,![]() 与
与![]() 可能相等,但
可能相等,但![]() 与
与![]() 不可能相等,
不可能相等,![]() 与
与![]() 不可能相等,
不可能相等,
所以集合![]() ,
,![]() 中元素的个数是3个或4个,
中元素的个数是3个或4个,
所以![]() 或
或![]() ;
;
(3)因为![]() 是公差为
是公差为![]() 的等差数列,所以
的等差数列,所以![]() ,
,
①若![]() ,取
,取![]() ,数列
,数列![]() 满足:
满足:![]() 与
与![]() 较接近,且
较接近,且![]() ,
,
则![]() 中有2018个正数,满足题意;
中有2018个正数,满足题意;
②若![]() ,取
,取![]() ,得
,得![]() ,数列
,数列![]() 满足:
满足:![]() 与
与![]() 较接近,
较接近,
![]() ,
,
则![]() 中有2018个正数,满足题意;
中有2018个正数,满足题意;
③若![]() ,取
,取![]() ,且
,且![]() ,数列
,数列![]() 满足:
满足:![]() 与
与![]() 较接近,
较接近,
则![]() ,所以
,所以![]() ,
,
则![]() 中恰有1009个正数,满足题意;
中恰有1009个正数,满足题意;
④若![]() ,若存在数列
,若存在数列![]() 满足:
满足:![]() 与
与![]() 较接近,即为
较接近,即为![]() ,
,
可得![]() ,
,
则![]() 中无正数,不符合题意。
中无正数,不符合题意。
综上可得:![]() 的取值范围是
的取值范围是![]() .
.


 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案科目:高中数学 来源: 题型:
【题目】已知![]() 三个内角
三个内角![]() 所对的边分别是
所对的边分别是![]() ,若
,若![]() .
.
(1)求角![]() ;
;
(2)若![]() 的外接圆半径为2,求
的外接圆半径为2,求![]() 周长的最大值.
周长的最大值.
【答案】(1) ![]() ;(2)
;(2) ![]() .
.
【解析】试题分析:(1)由正弦定理将边角关系化为边的关系![]() ,再根据余弦定理求角
,再根据余弦定理求角![]() ,(2)先根据正弦定理求边,用角表示周长,根据两角和正弦公式以及配角公式化为基本三角函数,最后根据正弦函数性质求最大值.
,(2)先根据正弦定理求边,用角表示周长,根据两角和正弦公式以及配角公式化为基本三角函数,最后根据正弦函数性质求最大值.
试题解析:(1)由正弦定理得![]() ,
,
∴![]() ,∴
,∴![]() ,即
,即![]()
因为![]() ,则
,则![]() .
.
(2)由正弦定理![]()
∴![]() ,
, ![]() ,
, ![]() ,
,
∴周长![]()
![]()
![]()
![]()
![]()
![]()
∵![]() ,∴
,∴![]()
∴当![]() 即
即![]() 时
时![]()
∴当![]() 时,
时, ![]() 周长的最大值为
周长的最大值为![]() .
.
【题型】解答题
【结束】
18
【题目】经调查,3个成年人中就有一个高血压,那么什么是高血压?血压多少是正常的?经国际卫生组织对大量不同年龄的人群进行血压调查,得出随年龄变化,收缩压的正常值变化情况如下表:

其中:  ,
, ![]() ,
, ![]()

(1)请画出上表数据的散点图;
(2)请根据上表提供的数据,用最小二乘法求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;(
;(![]() 的值精确到0.01)
的值精确到0.01)
(3)若规定,一个人的收缩压为标准值的0.9~1.06倍,则为血压正常人群;收缩压为标准值的1.06~1.12倍,则为轻度高血压人群;收缩压为标准值的1.12~1.20倍,则为中度高血压人群;收缩压为标准值的1.20倍及以上,则为高度高血压人群.一位收缩压为180mmHg的70岁的老人,属于哪类人群?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知a∈R,函数f(x)=(-x2+ax)ex(x∈R).
(1)当a=2时,求函数f(x)的单调区间;
(2)若函数f(x)在(-1,1)上单调递增,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在如图所示的多面体ABCDE,AB∥DE,AB⊥AD,△ACD是正三角形.AD=DE=2AB=2,EC=2![]() ,F是CD的中点.
,F是CD的中点.

(1)求证AF∥平面BCE;
(2)求直线AD与平面BCE所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某职称晋级评定机构对参加某次专业技术考试的100人的成绩进行了统计,绘制了频率分布直方图(如图所示),规定80分及以上者晋级成功,否则晋级失败.

晋级成功 | 晋级失败 | 合计 | |
男 | 16 | ||
女 | 50 | ||
合计 |
(1)求图中![]() 的值;
的值;
(2)根据已知条件完成下面![]() 列联表,并判断能否有
列联表,并判断能否有![]() 的把握认为“晋级成功”与性别有关?
的把握认为“晋级成功”与性别有关?
(3)将频率视为概率,从本次考试的所有人员中,随机抽取4人进行约谈,记这4人中晋级失败的人数为![]() ,求
,求![]() 的分布列与数学期望
的分布列与数学期望![]() .
.
(参考公式:![]() ,其中
,其中![]() )
)
| 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
| 0.780 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 |
查看答案和解析>>
科目:高中数学 来源: 题型:
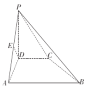
【题目】如下图,在四棱锥![]() 中,
中,![]() 面
面![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 为
为![]() 的中点。
的中点。
(1)求证:![]() 面
面![]() ;
;
(2)线段![]() 上是否存在一点
上是否存在一点![]() ,满足
,满足![]() ?若存在,试求出二面角
?若存在,试求出二面角![]() 的余弦值;若不存在,说明理由。
的余弦值;若不存在,说明理由。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=![]() x2-(a+1)x+alnx+1
x2-(a+1)x+alnx+1
(Ⅰ)若x=3是f(x)的极值点,求f(x)的极大值;
(Ⅱ)求a的范围,使得f(x)≥1恒成立.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】[选修4-4:坐标系与参数方程]
在直角坐标系![]() 中,点
中,点![]() ,直线
,直线![]() 的参数方程为
的参数方程为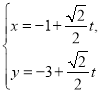 (
(![]() 为参数),曲线
为参数),曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以坐标原点为极点,
为参数),以坐标原点为极点,![]() 轴的正半轴为极轴建立极坐标系,已知曲线
轴的正半轴为极轴建立极坐标系,已知曲线![]() 的极坐标方程为
的极坐标方程为![]()
![]() ,直线
,直线![]() 与曲线
与曲线![]() 相交于
相交于![]() ,
,![]() 两点.
两点.
(1)求曲线![]() 与直线
与直线![]() 交点的极坐标(
交点的极坐标(![]() ,
,![]() );
);
(2)若![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com