
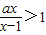 .
.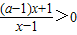 ,再对于字母a分情况讨论,即可求得解集.
,再对于字母a分情况讨论,即可求得解集.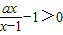
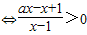
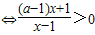
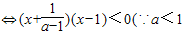 ,
,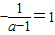 ,即a=0时,原不等式等价于(x-1)2<0⇒x∈ϕ;----(6分)
,即a=0时,原不等式等价于(x-1)2<0⇒x∈ϕ;----(6分)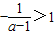 ,即a>0时,原不等式等价于
,即a>0时,原不等式等价于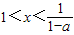 ;---------------(8分)
;---------------(8分)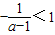 ,即a<0时,原不等式等价于
,即a<0时,原不等式等价于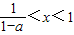 .---------------(10分)
.---------------(10分)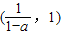 ;---------------------------------------(11分)
;---------------------------------------(11分)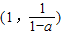 .----------------------------------------(13分)
.----------------------------------------(13分)

 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案 ABC考王全优卷系列答案
ABC考王全优卷系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com