
 的图象与
的图象与 轴的两个相邻交点的距离等于
轴的两个相邻交点的距离等于 ,则为得到函数
,则为得到函数 的图象可以把函数
的图象可以把函数 的图象上所有的点( )
的图象上所有的点( )A.向右平移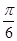 ,再将所得图象上所有的点的纵坐标变为原来的2倍 ,再将所得图象上所有的点的纵坐标变为原来的2倍 |
B.向右平移 ,再将所得图象上所有的点的纵坐标变为原来的2倍 ,再将所得图象上所有的点的纵坐标变为原来的2倍 |
C.向左平移 ,再将所得图象上所有的点的纵坐标变为原来的 ,再将所得图象上所有的点的纵坐标变为原来的 倍 倍 |
D.向左平移 ,再将所得图象上所有的点的纵坐标变为原来的2倍 ,再将所得图象上所有的点的纵坐标变为原来的2倍 |
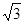 cosωx化为y=Asin(ωx+φ)的形式,再利用周期公式计算ω的值,最后由三角函数图象变换理论作出正确判断
cosωx化为y=Asin(ωx+φ)的形式,再利用周期公式计算ω的值,最后由三角函数图象变换理论作出正确判断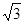 cosωx=2(
cosωx=2(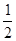 sinωx-
sinωx- 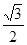 cosωx)=2sin(ωx-
cosωx)=2sin(ωx-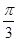 )
) ,
, =π
=π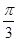 )=2sin2(x-
)=2sin2(x-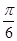 ),
),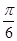 ,得y=sin2(x-
,得y=sin2(x-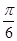 )的图象,再将所得图象上所有的点的纵坐标变为原来的2倍,得y=2sin2(x-
)的图象,再将所得图象上所有的点的纵坐标变为原来的2倍,得y=2sin2(x-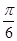 )的图象
)的图象

 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com