
(2005
广东,19)设函数f(x)在(-∞,+∞)上满足f(2-x)=f(2+x),f(7-x)=f(7+x),且在闭区间[0,7]上,只有f(1)=f(3)=0;(1)
试判断函数y=f(x)的奇偶性;(2)
试求方程f(x)=0在闭区间[-2005,2005]上的根的个数,并证明你的结论.|
解析:解法一: (1)若f(x)是偶函数,则f(-x)=f(2-(x+2))=f(2+(2+x))=f(4+x)=f(x),于是有f(7)=f(3)=0,这与f(x)在[0,7]上只有f(1)=f(3)=0矛盾!故f(x)不是偶函数.若 f(x)是奇函数,则f(0)=f(-0)=-f(0),有f(0)=0,这与在[0,7]上只有f(1)=f(3)=0矛盾!∴f(x)不是奇函数.故f(x)既不是偶函数,也不是奇函数.(2)∵f(x)=f[2 +(x-2)]=f[2-(x-2)]=f(4-x),f(x)=f[7 +(x-7)]=f[7-(x-7)]=f(14-x).∴f(14 -x)=f(4-x),即f[10+(4-x)]=f(4-x).∴f(x +10)=f(x).∴f(x)=f(x+10n),n Z. Z.
因此, f(1)=f(1+10n)=0,f(3)=f(3+10n)=0.即 x=10n+1和x=10n+3(n Z)均是f(x)=0的根. Z)均是f(x)=0的根.
由- 2005≤10n+1≤2005和-2005≤10n+3≤2005及n Z可得:n=0,±1,……,±200. Z可得:n=0,±1,……,±200.
故方程 f(x)=0在[-2005,2005]上的根至少有802个.如果存在 c (7,10)使f(c)=0,则f(14-c)=f(c)=0. (7,10)使f(c)=0,则f(14-c)=f(c)=0.
但 7>14-c≥4,这与f(x)在[0,7]上只有f(1)=f(3)=0矛盾!故f(x)=0在[0,10]上只有两个根,即x=1和x=3.设 d是f(x)=0在区间[-2005,2005]上任意一个根,则存在整数 n使d=10n+a,a [0,10], [0,10],
且 f(d)=f(10n+a)=f(a)=0.由上可知 a=1或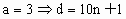 或d=10n+3. 或d=10n+3.
所以 f(x)=0在[-2005,2005]上有且仅有802个根.解法二: (1)∵f(x)在[0,7]上只有f(1)=f(3)=0.∴f(0) ≠0,即f(x)不是奇函数.∵f(2 -x)=f(2+x),f(x)关于x=2对称.∴f( -1)=f(5).而 f(5)≠0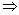 f(1)≠f(-1),即f(x)不是偶函数. f(1)≠f(-1),即f(x)不是偶函数.
故 f(x)是非奇非偶函数.(2) 由f(x)=f[2-(2-x)]=f[2+(2-x)]=f(4-x),有 f(x)=f[7-(3+x)]=f[7+(3+x)]=f(x+10).即 f(x)是周期为10的周期函数.∴f(7 -x)=f(7+x),∴f(x)关于x=7对称.∵f(x) 在[0,7]上仅有f(1)=f(3)=0,∴f(x) 在(7,10)上没有根.即 f(x)在[0,10]上仅x=1和x=3两个根.于是 f(x)在[0,2000]内仅有400个根,在[2000,2005]上仅有2根,在[-2000,0]内仅有400个根,而在[-2005,-2000]上没有根.故 f(x)在[-2005,2005]内仅有802个根. |
|
剖析:本小题主要考查函数的奇偶性、方程的根、解不等式等基础知识,以及函数与方程、分类与整合、化归与转化的数学思想方法,考查思维能力、运算能力. |


 阅读快车系列答案
阅读快车系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com