
已知a=(5 cos x,cos x),b=(sin x,2cos x),设函数f(x)=a·b+|b|2+
cos x,cos x),b=(sin x,2cos x),设函数f(x)=a·b+|b|2+ .
.
(1)当∈ 时,求函数f(x)的值域;
时,求函数f(x)的值域;
(2)当x∈ 时,若f(x)=8,求函数f
时,若f(x)=8,求函数f 的值;
的值;
(3)将函数y=f(x)的图象向右平移 个单位后,再将得到的图象上各点的纵坐标向下平移5个单位,得到函数y=g(x)的图象,求函数g(x)的表达式并判断奇偶性.
个单位后,再将得到的图象上各点的纵坐标向下平移5个单位,得到函数y=g(x)的图象,求函数g(x)的表达式并判断奇偶性.
(1)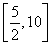 (2)
(2)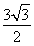 +7(3)g(x)=5sin 2x,g(x)为奇函数
+7(3)g(x)=5sin 2x,g(x)为奇函数
【解析】(1)f(x)=a·b+|b|2+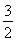
=5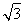 sin xcos x+2cos2x+4cos2x+sin2x+
sin xcos x+2cos2x+4cos2x+sin2x+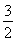 =5
=5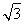 sin xcos x+5cos2x+
sin xcos x+5cos2x+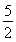
=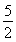
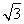 sin 2x+5×
sin 2x+5×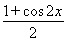 +
+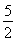 =5sin
=5sin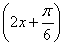 +5.
+5.
由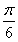 ≤x≤
≤x≤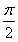 ,得
,得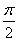 ≤2x+
≤2x+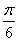 ≤
≤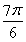 ,
,
∴-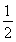 ≤sin
≤sin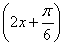 ≤1,∴当
≤1,∴当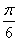 ≤x≤
≤x≤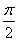 时,函数f(x)的值域为
时,函数f(x)的值域为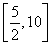 .
.
(2)f(x)=5sin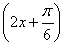 +5=8,
+5=8,
则sin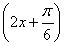 =
=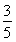 ,所以cos
,所以cos =-
=-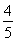 ,
,
f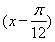 =5sin 2x+5=5sin
=5sin 2x+5=5sin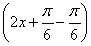 +5=
+5=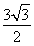 +7.
+7.
(3)由题意知f(x)=5sin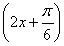 +5→g(x)=5sin
+5→g(x)=5sin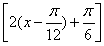 +5-5=5sin 2x,
+5-5=5sin 2x,
即g(x)=5sin 2x,
g(-x)=5sin(-2x)=-5sin 2x=-g(x),
故g(x)为奇函数.


科目:高中数学 来源:2014年高考数学(文)二轮专题复习与测试专题4第1课时练习卷(解析版) 题型:填空题
已知三棱柱ABC-A1B1C1,底面是边长为 的正三角形,侧棱垂直于底面,且该三棱柱的外接球的体积为
的正三角形,侧棱垂直于底面,且该三棱柱的外接球的体积为 ,则该三棱柱的体积为________.
,则该三棱柱的体积为________.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(文)二轮专题复习与测试专题2第3课时练习卷(解析版) 题型:填空题
在△ABC中,∠B=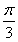 ,O为△ABC的外心,P为劣弧AC上一动点,且
,O为△ABC的外心,P为劣弧AC上一动点,且 =x
=x  +y
+y  (x,y∈R),则x+y的取值范围为________.
(x,y∈R),则x+y的取值范围为________.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(文)二轮专题复习与测试专题2第2课时练习卷(解析版) 题型:解答题
设函数f(x)=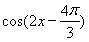 +2cos2x.
+2cos2x.
(1)求f(x)的最大值,并写出使f(x)取最大值时x的集合;
(2)已知△ABC中,角A,B,C的对边分别为a,b,c,若f(B+C)= ,b+c=2,求a的最小值.
,b+c=2,求a的最小值.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(文)二轮专题复习与测试专题2第2课时练习卷(解析版) 题型:选择题
已知cos α= ,cos(α+β)=-
,cos(α+β)=- ,且α,β∈
,且α,β∈ ,则cos(α-β)的值等于( )
,则cos(α-β)的值等于( )
A.- B.
B. C.-
C.- D.
D.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(文)二轮专题复习与测试专题1第6课时练习卷(解析版) 题型:解答题
已知函数f(x)= m(x-1)2-2x+3+ln x,m≥1.
m(x-1)2-2x+3+ln x,m≥1.
(1)当m= 时,求函数f(x)在区间[1,3]上的极小值;
时,求函数f(x)在区间[1,3]上的极小值;
(2)求证:函数f(x)存在单调递减区间[a,b];
(3)是否存在实数m,使曲线C:y=f(x)在点P(1,1)处的切线l与曲线C有且只有一个公共点?若存在,求出实数m的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(文)二轮专题复习与测试专题1第4课时练习卷(解析版) 题型:解答题
首届世界低碳经济大会在南昌召开,本届大会以“节能减排,绿色生态”为主题.某单位在国家科研部门的支持下,进行技术攻关,采用了新工艺,把二氧化碳转化为一种可利用的化工产品.已知该单位每月的处理量最少为400吨,最多为600吨,月处理成本y(元)与月处理量x(吨)之间的函数关系可近似地表示为y=x2-200x+80 000,且每处理一吨二氧化碳得到可利用的化工产品价值为100元.
(1)该单位每月处理量为多少吨时,才能使每吨的平均处理成本最低?
(2)该单位每月能否获利?如果获利,求出最大利润;如果不获利,则国家至少需要补贴多少元才能使该单位不亏损?
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(文)二轮专题复习与测试专题1第1课时练习卷(解析版) 题型:选择题
已知命题p:x2+2x-3>0;命题q:x>a,且?q的一个充分不必要条件是?p,则a的取值范围是( )
A.a≥1 B.a≤1
C.a≥-1 D.a≤-3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com