
 =
= +
+ +
+ ,且
,且 •
• =8,则边AC上的高h的最大值为 .
=8,则边AC上的高h的最大值为 . 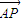 •
•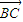 =0,将
=0,将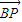 •
•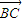 化简为
化简为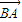 •
•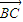 =8,结合∠B=60°算出
=8,结合∠B=60°算出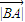 •
•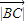 和三角形ABC的面积.利用余弦定理,算出当且仅当
和三角形ABC的面积.利用余弦定理,算出当且仅当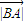 =
=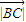 =4时,
=4时,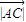 有最小值为4,结合三角形面积为4
有最小值为4,结合三角形面积为4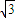 ,可得AC上的高h的最大值为2
,可得AC上的高h的最大值为2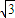 .
.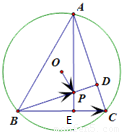 解:∵O为△ABC的外心,
解:∵O为△ABC的外心,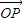 =
=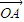 +
+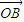 +
+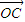 ,
,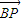 •
•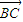 =(
=(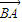 +
+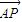 )
)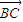 =8
=8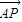 •
•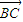 =0,∴
=0,∴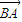 •
•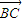 =8
=8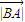 •
•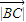 cos60°=8,得
cos60°=8,得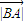 •
•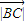 =16
=16
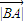 •
•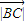 sin60°=4
sin60°=4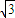
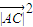 =
=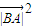 +
+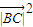 -2
-2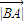 •
•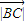 cos60°=
cos60°=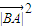 +
+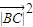 -16
-16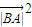 +
+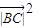 ≥2
≥2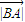 •
•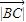 =32
=32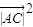 ≥16,得当且仅当
≥16,得当且仅当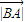 =
=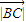 =4时,
=4时,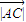 有最小值为4
有最小值为4
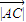 •h=4
•h=4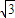 ,h是边AC上的高
,h是边AC上的高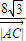 =2
=2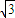 ,当且仅当
,当且仅当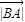 =
=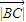 =
=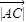 =4时,边AC上的高h的最大值为2
=4时,边AC上的高h的最大值为2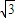


科目:高中数学 来源:2009-2010学年数学寒假作业(06)(解析版) 题型:解答题
 -1)c.
-1)c. ,
, ]时,函数f(x)=cos2x+asinx的最大值为3,求△ABC的面积.
]时,函数f(x)=cos2x+asinx的最大值为3,求△ABC的面积.查看答案和解析>>
科目:高中数学 来源:2011年浙江省绍兴市高三质量调研数学试卷(理科)(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com