已知公差d大于零的等差数列{an}(n∈N*)的前n项和为Sn,且满足:a3?a4=35,S3=9.
(1)求通项an;
(2)当a1b1+a2b2+a3b3+…+anbn=(2n-3)•2n+4(n∈N*),求数列{bn}的前n项和Tn.
解:(1)由已知,
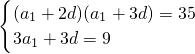
解得a
1=1,d=2,
∴a
n=2n-1
(2)由题意a
1b
1+a
2b
2+a
3b
3+…+a
nb
n=(2n-3)•2
n+4①
可得a
1b
1+a
2b
2+a
3b
3+…+a
nb
n +a
n+1b
n+1=[2(n+1)-3]•2
n+1+4②
②-①得a
n+1b
n+1=2
n(2n+1),又a
n+1=2n+1
∴b
n+1=2
n,
又a
1b
1=(2-3)•2+4=2,可得b
1=2,故b
n=
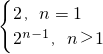
.
数列{b
n}是从第二项开始以b
2=2为首项,以2为公比的等比数列,首项b
1=2,
T
n=2+2×
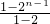
=2
n分析:(1)利用等差数列通项公式及前n项和公式 列出关于a
1,d方程组并解出a
1,d后,即可求出通项a
n.
(2)由a
1b
1+a
2b
2+a
3b
3+…+a
nb
n=(2n-3)•2
n+4①得出a
1b
1+a
2b
2+a
3b
3+…+a
nb
n +a
n+1b
n+1=[2{n+1)-3]•2
n+1+4②
两式相减,求出 b
n=2
n-1.再利用等比数列求和公式计算.
点评:本题考查等差数列通项公式及前n项和公式,等比数列的判定及前n项和公式.对a
1b
1+a
2b
2+a
3b
3+…+a
nb
n=(2n-3)•2
n+4 看作数列{a
nb
n}和的表达式,类比于数列中a
n 与 Sn的关系,求出a
n+1b
n+1=2n(2n+1),b
n+1=2
n是关键.

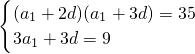 解得a1=1,d=2,
解得a1=1,d=2,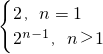 .
.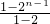 =2n
=2n
