Question

（本小题满分13分）一车间生产A， B， C三种样式的LED节能灯，每种样式均有10W和30W两种型号，某天的产量如右表(单位：个)：

按样式分层抽样的方法在这个月生产的灯泡中抽取100个，其中有A样式灯泡25个。

（1）求z的值；

（2）用分层抽样的方法在A样式灯泡中抽取一个容量为5的样本，从这个样本中任取2个灯泡，求至少有1个10W的概率．

型号	A样式	B样式	C样式
10W	2000	z	3000
30W	3000	4500	5000

 

 

Answer 1

【答案】

（1）z＝2500；（2）。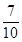

【解析】

试题分析：(1).设该厂本月生产的B样式的灯泡为n个,在C样式的灯泡中抽取x个，由题意得,

,所以x="40." ……2分

则100－40－25＝35，所以，

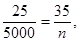n=7000，        

故z＝2500  ……7分

(2) 设所抽样本中有m个10W的灯泡,

因为用分层抽样的方法在A样式灯泡中抽取一个容量为5的样本,

所以,解得m=2  ……9分

也就是抽取了2个10W的灯泡,3个30W的灯泡,

分别记作S₁,S₂;B_1,B₂,B₃,则从中任取2个的所有基本事件为

(S₁, B₁), (S₁, B₂) , (S₁, B₃) (S₂ ,B₁), (S₂ ,B₂), (S₂ ,B₃),( (S₁, S₂),(B₁ ,B₂), (B₂ ,B₃) ,(B₁ ,B₃)

共10个,    ……10分

其中至少有1个10W的灯泡的基本事件有7个基本事件：……11分

(S₁, B₁), (S₁, B₂) , (S₁, B₃) (S₂ ,B₁), (S₂ ,B₂), (S₂ ,B₃),( (S₁, S₂),所以从中任取2个,至少有1个10W的灯泡的概率为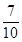．……13分

考点：分层抽样；随机事件的概率；古典概型。

点评：本题考查列举法计算基本事件数及随机事件发生的概率，解题的关键是熟练运用分类列举的方法及事件的性质将所有的基本事件一一列举出来，运用公式求出概率，列举法求概率适合基本事件数不太多的概率求解问题。