
(2012年高考(广东理))设数列![]() 的前
的前![]() 项和为
项和为![]() ,满足
,满足![]() ,
,![]()
![]() ,且
,且![]() 、
、![]() 、
、![]() 成等差数列.
成等差数列.
(Ⅰ)求![]() 的值;
的值;
(Ⅱ)求数列![]() 的通项公式;
的通项公式;
(Ⅲ)证明:对一切正整数![]() ,有
,有![]() .
.
解析:(Ⅰ)由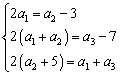 ,解得
,解得![]() .
.
(Ⅱ)由![]() 可得
可得![]() (
(![]() ),两式相减,可得
),两式相减,可得![]() ,即
,即![]() ,即
,即![]() ,所以数列
,所以数列![]() (
(![]() )是一个以
)是一个以![]() 为首项,3为公比的等比数列.由
为首项,3为公比的等比数列.由![]() 可得,
可得,![]() ,所以
,所以![]() ,即
,即![]() (
(![]() ),当
),当![]() 时,
时,![]() ,也满足该式子,所以数列
,也满足该式子,所以数列![]() 的通项公式是
的通项公式是![]() .
.
(Ⅲ)因为![]() ,所以
,所以![]() ,所以
,所以![]() ,于是
,于是 .
.
点评:上述证法实质上是证明了一个加强命题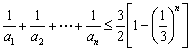 ,该加强命题的思考过程如下.
,该加强命题的思考过程如下.
考虑构造一个公比为![]() 的等比数列
的等比数列![]() ,其前
,其前![]() 项和为
项和为![]() ,希望能得到
,希望能得到![]() ,考虑到
,考虑到![]() ,所以令
,所以令![]() 即可.由
即可.由![]() 的通项公式的形式可大胆尝试令
的通项公式的形式可大胆尝试令![]() ,则
,则![]() ,于是
,于是![]() ,此时只需证明
,此时只需证明![]() 就可以了.
就可以了.
当然,![]() 的选取并不唯一,也可令
的选取并不唯一,也可令![]() ,此时
,此时![]() ,
,![]() ,与选取
,与选取![]() 不同的地方在于,当
不同的地方在于,当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ,所以此时我们不能从第一项就开始放缩,应该保留前几项,之后的再放缩,下面给出其证法.
,所以此时我们不能从第一项就开始放缩,应该保留前几项,之后的再放缩,下面给出其证法.
当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() .
.
当![]() 时,
时,![]() ,所以
,所以
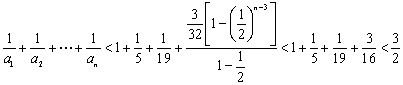 .
.
综上所述,命题获证.
下面再给出![]() 的两个证法.
的两个证法.
法1:(数学归纳法)
①当![]() 时,左边
时,左边![]() ,右边
,右边![]() ,命题成立.
,命题成立.
②假设当![]() (
(![]() ,
,![]()
![]() )时成立,即
)时成立,即![]() 成立.为了证明当
成立.为了证明当![]() 时命题也成立,我们首先证明不等式:
时命题也成立,我们首先证明不等式:![]() (
(![]() ,
,![]()
![]() ).
).
要证![]() ,只需证
,只需证![]() ,只需证
,只需证![]() ,只需证
,只需证![]() ,只需证
,只需证![]() ,该式子明显成立,所以
,该式子明显成立,所以![]() .
.
于是当![]() 时,
时,![]() ,所以命题在
,所以命题在![]() 时也成立.
时也成立.
综合①②,由数学归纳法可得,对一切正整数![]() ,有
,有![]() .
.
备注:不少人认为当不等式的一边是常数的时候是不能用数学归纳法的,其实这是一个错误的认识.
法2:(裂项相消法)(南海中学钱耀周提供)
当![]() 时,
时,![]() 显然成立.当
显然成立.当![]() 时,
时,![]() 显然成立.
显然成立.
当![]() 时,
时,![]()
![]()
![]() ,又因为
,又因为![]() ,所以
,所以![]() (
(![]() ),所以
),所以![]() (
(![]() ),所以
),所以
![]() .
.
综上所述,命题获证.


 阅读快车系列答案
阅读快车系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com