考点:用空间向量求平面间的夹角,用空间向量求直线间的夹角、距离
专题:空间位置关系与距离,空间角
分析:(1)以点A为坐标原点,AB,AC,AA1分别为x,y,z轴,建立空间直角坐标系,利用向量法能求出棱CC1的长.
(2)求出平面PAB的一个法向量,和平面ABB1的一个法向量,由已知条件利用向量法能求出λ的值.
解答:
解:(1)以点A为坐标原点,AB,AC,AA
1分别为x,y,z轴,
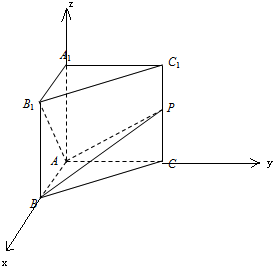
建立空间直角坐标系,
设CC
1=m,则B
1(3,0,m),
B(3,0,0),P(0,4,λm),
所以
=(3,0,m),
=(3,-4,-λm),
=(3,0,0),…2分
当
λ=时,有
•=(3,0,m)•(3,-4,-m)=0解得
m=3,即棱CC
1的长为
3.…4分
(2)设平面PAB的一个法向量为
=(x,y,z),
则由
,得
,即
,
令z=1,则
y=-,
所以平面PAB的一个法向量为
=(0,-,1),…6分
又平面ABB
1与y轴垂直,所以平面ABB
1的一个法向量为
=(0,1,0),
因二面角B
1-AB-P的平面角的大小为
,
所以|cos<
,>|=
=|
|,
结合λ>0,解得
λ=.…10分.
点评:本题考查线段长的求法,考查实数值的求法,解题时要认真审题,注意向量法的合理运用,是中档题.

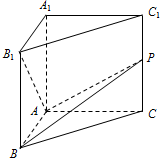 如图,在直三棱柱ABC-A1B1C1中,AB⊥AC,AB=3,AC=4,动点P满足
如图,在直三棱柱ABC-A1B1C1中,AB⊥AC,AB=3,AC=4,动点P满足


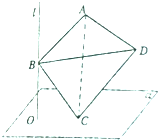 如图,直线l⊥平面α,垂足为O,正四面体ABCD的棱长为8,C在平面α内,B是直线l上的动点,则当O到AD的距离为最大时,正四面体在平面α上的射影面积为( )
如图,直线l⊥平面α,垂足为O,正四面体ABCD的棱长为8,C在平面α内,B是直线l上的动点,则当O到AD的距离为最大时,正四面体在平面α上的射影面积为( )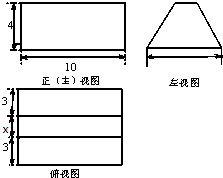 现制作三视图如图所示的几何体的模型,为了配合原料,需要计算该模型的体积,而给出的俯视图中的x位置的数据丢失,但已知该模型的表面积为240,则该模型的体积为( )
现制作三视图如图所示的几何体的模型,为了配合原料,需要计算该模型的体积,而给出的俯视图中的x位置的数据丢失,但已知该模型的表面积为240,则该模型的体积为( )