
| A. | 4 | B. | $\frac{8}{3}$ | C. | $\frac{4\sqrt{3}}{3}$ | D. | $\frac{4}{3}$ |
分析 如图所示,取BC的中点D,连接AD,SD,则SD⊥BC,AD⊥BC.由题意,AS⊥平面SBC,SA=2,SD=$\sqrt{3}$,AG=2GD=$\frac{2\sqrt{7}}{3}$,cos∠SAD=$\frac{2}{\sqrt{7}}$.利用余弦定理可得|$\overrightarrow{SG}$|.
解答 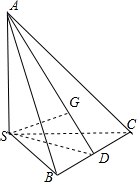 解:如图所示,取BC的中点D,连接AD,SD,则SD⊥BC,AD⊥BC.
解:如图所示,取BC的中点D,连接AD,SD,则SD⊥BC,AD⊥BC.
由题意,AS⊥平面SBC,SA=2,SD=$\sqrt{3}$,AG=2GD=$\frac{2\sqrt{7}}{3}$,cos∠SAD=$\frac{2}{\sqrt{7}}$.
由余弦定理可得|$\overrightarrow{SG}$|=$\sqrt{4+\frac{28}{9}-2×2×\frac{2\sqrt{7}}{3}×\frac{2}{\sqrt{7}}}$=$\frac{4}{3}$,
故选D.
点评 本题考查棱锥的结构特征,考查线面垂直,考查余弦定理的运用,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | S2016=2016,a2010<a7 | B. | S2016=2016,a2010>a7 | ||
| C. | S2016=-2016,a2010<a7 | D. | S2016=-2016,a2010>a7 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ?x>0,使2x>10 | B. | ?x>0,使2x≤10 | C. | ?x≤0,使2x≤10 | D. | ?x≤0,使2x>10 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,经过村庄A有两条互相垂直的笔直公路AB和AC,根据规划拟在两条公路围成的直角区域内建一工厂P,为了仓库存储和运输方便,在两条公路上分别建两个仓库M,N(异于村庄A,将工厂P及仓库M,N近似看成点,且M,N分别在射线AB,AC上),要求MN=2,PN=1(单位:km),PN⊥MN.
如图,经过村庄A有两条互相垂直的笔直公路AB和AC,根据规划拟在两条公路围成的直角区域内建一工厂P,为了仓库存储和运输方便,在两条公路上分别建两个仓库M,N(异于村庄A,将工厂P及仓库M,N近似看成点,且M,N分别在射线AB,AC上),要求MN=2,PN=1(单位:km),PN⊥MN.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 微信群数量 | 频数 | 频率 |
| 0至5个 | 0 | 0 |
| 6至10个 | 30 | 0.3 |
| 11至15个 | 30 | 0.3 |
| 16至20个 | a | c |
| 20个以上 | 5 | b |
| 合计 | 100 | 1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com