
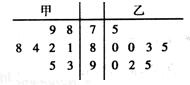
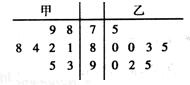
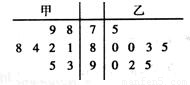
 上海世博会在游客入园参观的试运营阶段,为了解每个入口的通行速度,在一号入口处随机抽取甲、乙两名安检人员在一小时内完成游客入园人数的8次记录,记录人数的茎叶图如图:
上海世博会在游客入园参观的试运营阶段,为了解每个入口的通行速度,在一号入口处随机抽取甲、乙两名安检人员在一小时内完成游客入园人数的8次记录,记录人数的茎叶图如图: 甲=
甲= (70×2+80×4+90×2+8+9+1+2+4+8+3+5)=85,
(70×2+80×4+90×2+8+9+1+2+4+8+3+5)=85, (70×1+80×4+90×3+5+0+0+3+5+0+2+5)=85,
(70×1+80×4+90×3+5+0+0+3+5+0+2+5)=85,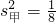 [(78-85)2+(79-85)2+(81-85)2+(82-85)2+(84-85)2+(88-85)2
[(78-85)2+(79-85)2+(81-85)2+(82-85)2+(84-85)2+(88-85)2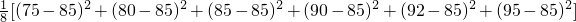 =41
=41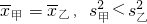 ,
,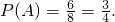
 ).
).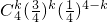 (k=0,1,2,3,4)
(k=0,1,2,3,4)
 =3
=3 ).这样代入公式,可以求出变量对应的事件的概率,写出分布列和期望.
).这样代入公式,可以求出变量对应的事件的概率,写出分布列和期望.

科目:高中数学 来源: 题型:
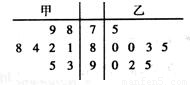
 上海世博会在游客入园参观的试运营阶段,为了解每个入口的通行速度,在一号入口处随机抽取甲、乙两名安检人员在一小时内完成游客入园人数的8次记录,记录人数的茎叶图如图:
上海世博会在游客入园参观的试运营阶段,为了解每个入口的通行速度,在一号入口处随机抽取甲、乙两名安检人员在一小时内完成游客入园人数的8次记录,记录人数的茎叶图如图:查看答案和解析>>
科目:高中数学 来源:2010年湖南省长沙一中高考数学三模试卷(理科)(解析版) 题型:解答题
查看答案和解析>>
科目:高中数学 来源:2011-2012学年湖南省邵阳市洞口二中高三(下)集中训练数学试卷3(理科)(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com