
分析 根据题意得出P,Q两点间的最短距离为直角△SOC斜边SC上的高OM,求出即可.
解答 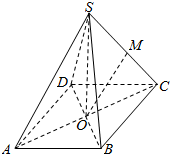 解:如图所示,
解:如图所示,
四棱锥S-ABCD底面为正方形,边长为$\sqrt{2}$,且SA=SB=SC=SD,高为SO=2,
P,Q两点分别在线段BD,SC上,
则P,Q两点间的最短距离为直角三角形SOC斜边SC上的高OM;
所以OM=$\frac{OS•OC}{SC}$=$\frac{2×\frac{1}{2}\sqrt{{(\sqrt{2})}^{2}{+(\sqrt{2})}^{2}}}{\sqrt{{2}^{2}{+1}^{2}}}$=$\frac{2\sqrt{5}}{5}$.
故答案为:$\frac{2\sqrt{5}}{5}$.
点评 本题考查了空间几何体结构特征的应用问题,也考查了空间想象能力的应用问题,是基础题目.


 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=±$\frac{1}{2}$x | B. | y=±$\frac{\sqrt{2}}{2}$x | C. | y=±$\frac{1}{3}$x | D. | y=±$\frac{\sqrt{3}}{3}$x |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
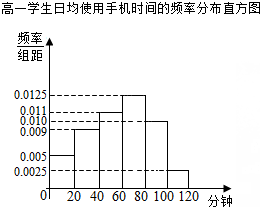 某学校为了了解学生使用手机的情况,分别在高一和高二两个年级各随机抽取了100名学生进行调查.下面是根据调查结果绘制的学生日均使用手机时间的频率分布直方图和频数分布表,将使用手机时间不低于80分钟的学生称为“手机迷”.
某学校为了了解学生使用手机的情况,分别在高一和高二两个年级各随机抽取了100名学生进行调查.下面是根据调查结果绘制的学生日均使用手机时间的频率分布直方图和频数分布表,将使用手机时间不低于80分钟的学生称为“手机迷”.| 时间分组 | 频数 |
| [0,20) | 12 |
| [20,40) | 20 |
| [40,60) | 24 |
| [60,80) | 26 |
| [80,100) | 14 |
| [100,120] | 4 |
| 非手机迷 | 手机迷 | 合计 | |
| 男 | 30 | 15 | 45 |
| 女 | 45 | 10 | 55 |
| 合计 | 75 | 25 | 100 |
| 参考数据 | P(k2≥x0) | 0.15 | 0.10 | 0.05 | 0.025 |
| x0 | 2.072 | 2.706 | 3.841 | 5.024 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com