
| |||||||||||
(1) |
解:∵f(x)≥x的解集为R ∴x2-(4a+1)x+a2≥0对于x∈R恒成立…………2分 ∴△=(4a+1)2-4a2≤0 即12a2+8a+1≤0…………4分 (2a+1)(6a+1)≤0 ∴― ∴a的取值范围为[― |
(2) |
解:∵g(x)=2x3+3ax2-12a2x+3a2在(-1,+∞)内单调递增 ∴g′(x)=6x2+6ax-12a2≥0在(-1,+∞)内恒成立………7分 ∵二次函数g′(x)图象的对称轴为x=- ①当- ∴f(x)在(-1,+∞)不能单调递增…………10分 ②当-
综上所述,a的取值范围为 |


科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源:2004全国各省市高考模拟试题汇编(天利38套)·数学 题型:044
已知函数f(x)=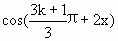 +
+ (k∈Z)
(k∈Z)
(1)化简f(x)并求f(x)的最小正周期.
(2)当k=1时,f(x)的图像可由函数y=2sin2x的图像经过怎样的变换得到?
查看答案和解析>>
科目:高中数学 来源:2005年广东省广州市高二数学水平测试试卷(解析版) 题型:解答题
查看答案和解析>>
科目:高中数学 来源:2005年广东省广州市普通高中必修模块调研数学试卷(11月份)(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com