
(2006
·湖南益阳)如下图,已知长方体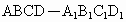 ,AB=2,
,AB=2,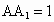 ,直线BD与平面
,直线BD与平面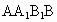 所成的角为30°,AE垂直BD于E,F为
所成的角为30°,AE垂直BD于E,F为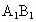 的中点.
的中点.
(1)
求异面直线AE与BF所成的角的余弦值;(2)
求平面BDF与平面 所成的锐二面角的余弦值;
所成的锐二面角的余弦值;
(3)
求点A到平面BDF的距离.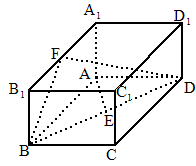
|
证明:在长方体 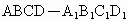 中,以AB所在的直线为x轴,以AD所在的直线为y轴, 中,以AB所在的直线为x轴,以AD所在的直线为y轴,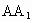 所在的直线为z轴建立空间直角坐标系,由已知AB=2, 所在的直线为z轴建立空间直角坐标系,由已知AB=2,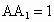 ,可得A(0,0,0),B(2,0,0),F(1,0,1). ,可得A(0,0,0),B(2,0,0),F(1,0,1).
又 AD⊥平面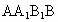 ,从而BD与平面 ,从而BD与平面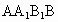 所成的角为∠DBA=30°,又AB=2,AE⊥BD,AE=1, 所成的角为∠DBA=30°,又AB=2,AE⊥BD,AE=1,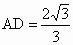 ,从而易得 ,从而易得 , ,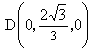 . .
(1)因为 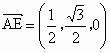 , ,所以 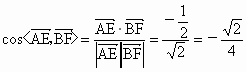 .易知异面直线AE、BF所成的角的余弦值是 .易知异面直线AE、BF所成的角的余弦值是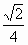 . .
(2) 易知平面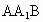 的一个法向量m=(0,1,0),设n(x,y,z)是平面BDF的一个法向量, 的一个法向量m=(0,1,0),设n(x,y,z)是平面BDF的一个法向量,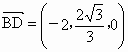 . .
由 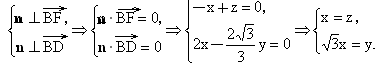
即  ,即平面BDF与平面 ,即平面BDF与平面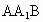 所成的锐二面角的余弦值是 所成的锐二面角的余弦值是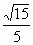 . .
(3) 点A到平面BDF的距离,即所以距离 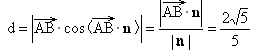 .所以点A到平面BDF的距离为 .所以点A到平面BDF的距离为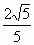 . . |


 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com