
已知函数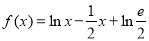 ,
,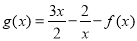 .
.
(1)求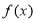 的单调区间;
的单调区间;
(2)设函数 ,若存在
,若存在 ,对任意的
,对任意的 ,总有
,总有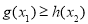 成立,求实数
成立,求实数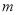 的取值范围.
的取值范围.
(1)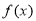 的单调增区间为
的单调增区间为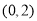 ,单调减区间为
,单调减区间为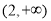 ;(2)实数
;(2)实数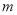 的取值范围为
的取值范围为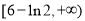 .
.
【解析】
试题分析:(1)首先确定函数的定义域,进一步对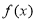 求导,利用导函数与原函数的关系,得到原函数的单调区间;(2)“存在
求导,利用导函数与原函数的关系,得到原函数的单调区间;(2)“存在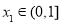 ,对任意的
,对任意的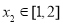 ,总有
,总有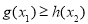 成立”等价于“
成立”等价于“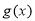 在
在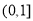 上的最大值不小于
上的最大值不小于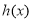 在
在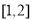 上的最大值”进一步,分别求函数
上的最大值”进一步,分别求函数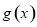 和
和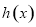 在区间
在区间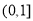 和
和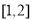 上的最大值.
上的最大值.
试题解析:(1)  ,(此处若不写定义域,可适当扣分)
,(此处若不写定义域,可适当扣分)
故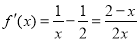 .
.
 当
当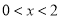 时,
时, ;当
;当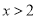 时,
时,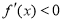 .
.

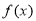 的单调增区间为
的单调增区间为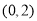 ,单调减区间为
,单调减区间为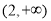 ;
;
(2)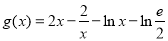 ,则
,则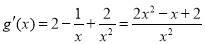 ,
,
而 ,故在
,故在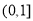 上
上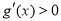 ,即函数
,即函数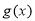 在
在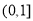 上单调递增,
上单调递增,
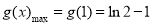
而“存在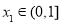 ,对任意的
,对任意的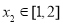 ,总有
,总有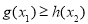 成立”等价于“
成立”等价于“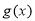 在
在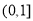 上的最大值不小于
上的最大值不小于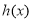 在
在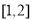 上的最大值”
上的最大值”
而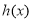 在
在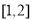 上的最大值为
上的最大值为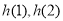 中的最大者,记为
中的最大者,记为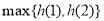 .
.
所以有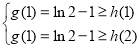 ,
,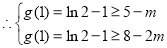 ,
,
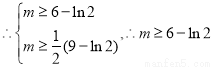 .
.
故实数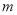 的取值范围为
的取值范围为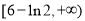 .
.
考点:1.利用导函数求单调性;2.函数的最值.


科目:高中数学 来源:2014-2015学年广东省高一上学期期中考试数学试卷(解析版) 题型:选择题
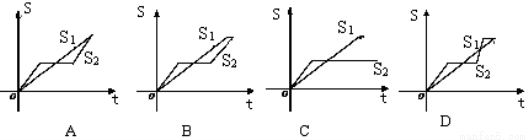
“龟兔赛跑”讲述了这样的故事:领先的兔子看着慢慢爬行的乌龟,骄傲起来,睡了一觉,当它醒来时,发现乌龟快到终点了,于是急忙追赶,但为时已晚,乌龟还是先到达了终点…用S1、S2分别表示乌龟和兔子所行的路程,t为时间,则与故事情节相吻合是( )
查看答案和解析>>
科目:高中数学 来源:2014-2015学年甘肃省高二上学期期末考试理科数学卷(解析版) 题型:选择题
设 表示三条不同的直线,
表示三条不同的直线,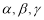 表示三个不同的平面,给出下列四个命题:
表示三个不同的平面,给出下列四个命题:
①若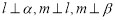 ,则
,则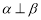 ;
;
②若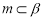 ,
,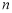 是
是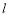 在
在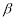 内的射影,
内的射影,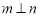 ,则
,则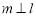 ;
;
③若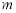 是平面
是平面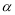 的一条斜线,
的一条斜线,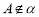 ,
,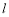 为过
为过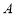 的一条动直线,则可能有
的一条动直线,则可能有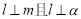 ;
;
④若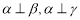 ,则
,则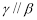
其中真命题的个数为( )个
(A)1 (B)2 (C)3 (D)4
查看答案和解析>>
科目:高中数学 来源:2014-2015学年山东省高三上学期第二次阶段性检测理科数学试卷(解析版) 题型:解答题
命题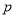 实数
实数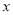 满足
满足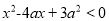 (其中
(其中 ),命题
),命题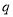 实数
实数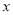 满足
满足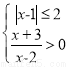
(1)若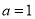 ,且
,且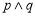 为真,求实数
为真,求实数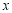 的取值范围;
的取值范围;
(2)若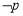 是
是
 的充分不必要条件,求实数
的充分不必要条件,求实数 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com