
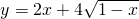 的值域是________,
的值域是________,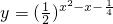 的值域是________.函数
的值域是________.函数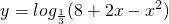 的值域是________.
的值域是________. ] [-2,+∞)
] [-2,+∞)
 =2(1-t2)+4t
=2(1-t2)+4t =(x-
=(x- )2-
)2- ,
, 为对称轴的二次函数,
为对称轴的二次函数, ,即g(x)≥-
,即g(x)≥- ,
, 时,函数y=
时,函数y= 有最大值为
有最大值为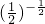 =
= ,
, ].
]. 有最小值为
有最小值为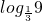 =-2,
=-2,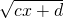 模型的函数,求值域事宜采用换元法.
模型的函数,求值域事宜采用换元法.

科目:高中数学 来源: 题型:
A.该函数的值域是[-1,1]
B.当且仅当x=2kπ+![]() (k∈Z)时,函数取得最大值1
(k∈Z)时,函数取得最大值1
C.该函数是以π为最小正周期的周期函数
D.当且仅当2kπ+π<x<2kπ+![]() (k∈Z)时,f(x)<0
(k∈Z)时,f(x)<0
查看答案和解析>>
科目:高中数学 来源:2015届浙江省湖州市高一12月月考数学试卷(解析版) 题型:解答题
已知函数
(1)判断函数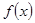 的单调性并用函数单调性定义加以证明;
的单调性并用函数单调性定义加以证明;
(2)若 在
在 上的值域是
上的值域是 ,求
,求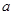 的值;
的值;
(3)当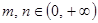 ,若
,若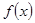 在
在 上的值域是
上的值域是
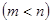 ,求实数
,求实数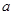 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源:2014届浙江省高一12月阶段性检测数学试卷 题型:填空题
下列几个命题:
①方程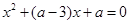 的有一个正实根,一个负实根,则
的有一个正实根,一个负实根,则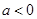 ;
;
②函数 是偶函数,但不是奇函数;
是偶函数,但不是奇函数;
③函数 的值域是
的值域是 ,则函数
,则函数 的值域为
的值域为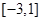 ;
;
④ 设函数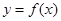 定义域为R,则函数
定义域为R,则函数 与
与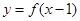 的图象关于
的图象关于 轴对称;
轴对称;
⑤一条曲线 和直线
和直线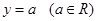 的公共点个数是
的公共点个数是 ,则
,则 的值不可能是1.
的值不可能是1.
其中正确的有___________________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com