
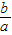 )m+(
)m+(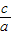 )m=1,由常数1联系同角三角函数的平方关系,可以设(
)m=1,由常数1联系同角三角函数的平方关系,可以设( )m=sin2θ;(
)m=sin2θ;(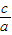 )m=cos2θ,(0°<θ<90°),又由题意,可得b+c>a,将b、c与a的关系代入可得,a•
)m=cos2θ,(0°<θ<90°),又由题意,可得b+c>a,将b、c与a的关系代入可得,a• +a•
+a•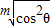 >a;进而整理变形可得,
>a;进而整理变形可得,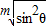 +
+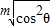 >1=sin2θ+cos2θ,结合幂函数的性质,分析可得答案.
>1=sin2θ+cos2θ,结合幂函数的性质,分析可得答案.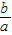 )m+(
)m+(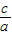 )m=1,且a>b,a>c;
)m=1,且a>b,a>c;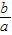 )m=sin2θ;(
)m=sin2θ;(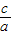 )m=cos2θ,(0°<θ<90°)
)m=cos2θ,(0°<θ<90°)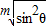 ,c=a•
,c=a•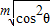 ;
;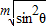 +a•
+a•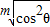 >a;
>a;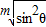 +
+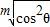 >1=sin2θ+cos2θ,
>1=sin2θ+cos2θ,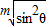 >sin2θ与
>sin2θ与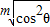 >cos2θ同时成立,
>cos2θ同时成立,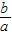 )m+(
)m+(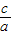 )m=1,由常数1联系同角三角函数的平方关系,是解题的突破口.
)m=1,由常数1联系同角三角函数的平方关系,是解题的突破口. 

 高中必刷题系列答案
高中必刷题系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com