
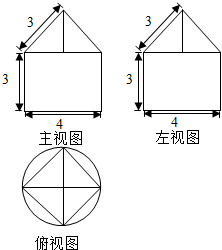
 一个空间几何体的三视图如图所示,根据图中数据:
一个空间几何体的三视图如图所示,根据图中数据:分析 (1)根据几何体的三视图,得出该几何体是圆柱与正四棱锥的组合体,结合图中数据画出它的直观图;
(2)该几何体的表面积是S圆柱+S棱锥侧面积-S棱锥底面积;
(3)该几何体的体积是V圆柱+V棱台.
解答 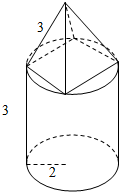 解:(1)根据几何体的三视图,得;
解:(1)根据几何体的三视图,得;
该几何体是下部为圆柱体,上部为正四棱锥的组合体,
且圆柱体的高为3,底面半径为2,
四棱锥的底面为圆柱底面圆的内接正四边形,棱长为3,
如图所示;
(2)该几何体的表面积为
S=S圆柱+S棱锥侧面积-S棱锥底面积
=(2π•22+2π•2•3)+4•$\frac{1}{2}$•2$\sqrt{2}$•$\sqrt{{3}^{2}{-(\sqrt{2})}^{2}}$-${(2\sqrt{2})}^{2}$
=20π+4$\sqrt{14}$-8;
(3)该几何体的体积为
V=V圆柱+V棱台
=π•22•3+$\frac{1}{3}$•${(2\sqrt{2})}^{2}$•$\sqrt{{3}^{2}{-2}^{2}}$
=12π+$\frac{8}{3}$$\sqrt{5}$.
点评 本题考查了空间几何体三视图的应用问题,也考查了作图能力的应用问题,考查了计算能力与空间想象能力的应用问题,是综合题目.


 考前必练系列答案
考前必练系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 归纳推理是由特殊到一般的推理 | B. | 演绎推理是由一般到特殊的推理 | ||
| C. | 类比推理是由特殊到一般的推理 | D. | 类比推理是由特殊到特殊的推理 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com