
| 3 |
| m |
| 3 |
| lim |
| n→∞ |
| (-2)n-3n |
| 3n+2n |
| 1 |
| n(n+2) |
| 3 |
| 4 |
| 1 |
| 2 |
| 2x+1 |
| x-1 |
| 3 |
| m |
| 3 |
| 3 |
| m |
| 3 |
| 3 |
| lim |
| n→∞ |
| (-2)n-3n |
| 3n+2n |
| lim |
| n→∞ |
(-
| ||
1+(
|
| 1 |
| n(n+2) |
| 1 |
| 2 |
| 1 |
| n |
| 1 |
| n+2 |
| 3 |
| 4 |
| 1 |
| 2 |
| 2n+3 |
| n2+3n+2 |
| lim |
| n→∞ |
| lim |
| n→∞ |
| 3 |
| 4 |
| 1 |
| 2 |
| 2n+3 |
| n2+3n+2 |
| 3 |
| 4 |
| 2x+1 |
| x-1 |
| 3 |
| m |
| 3 |
| 3 |
| m |
| 3 |
| 3 |
| lim |
| n→∞ |
| (-2)n-3n |
| 3n+2n |
| lim |
| n→∞ |
(-
| ||
1+(
|
| 1 |
| n(n+2) |
| 1 |
| 2 |
| 1 |
| n |
| 1 |
| n+2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 5 |
| 1 |
| 2 |
| 1 |
| n |
| 1 |
| n+2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| n+1 |
| 1 |
| n+2 |
| 3 |
| 4 |
| 1 |
| 2 |
| 2n+3 |
| n2+3n+2 |
| lim |
| n→∞ |
| lim |
| n→∞ |
| 3 |
| 4 |
| 1 |
| 2 |
| 2n+3 |
| n2+3n+2 |
| 3 |
| 4 |
| 2x+1 |
| x-1 |


 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案科目:高中数学 来源: 题型:
| 1 | 4 |
查看答案和解析>>
科目:高中数学 来源:“伴你学”新课程 数学·选修1-2(人教B版) 人教B版 题型:013
已知m、n是不重合的直线,α、β是不重合的平面,有下列命题:
(1)若m![]() α,n∥α,则m∥n;
α,n∥α,则m∥n;
(2)若m∥α,m∥β,则α∥β;
(3)若α∩β=n,m∥n,则m∥α且m∥β;
(4)若m⊥α,m⊥β,则α∥β.
其中真命题的个数是
0
1
2
3
查看答案和解析>>
科目:高中数学 来源:数学教研室 题型:013
已知m、n是两条不重合的直线,α、β、γ是三个两两不重合的平面,给出下列命题:
(1)若m∥β,n∥β且m α,n
α,n α,则α∥β;
α,则α∥β;
(2)若α∩β=n,m∥n,则m∥α且m∥β;
(3)若m⊥α,m∥β,则α⊥β;
(4)若α∥β,且γ∩α=m,γ∩β=n,则m∥n.
其中的正确命题是
[ ]
查看答案和解析>>
科目:高中数学 来源: 题型:013
已知
m、n是两条不重合的直线,α、β、γ是三个两两不重合的平面,给出下列命题:(1)
若m∥β,n∥β且m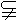 α,n
α,n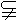 α,则α∥β;
α,则α∥β;
(2)
若α∩β=n,m∥n,则m∥α且m∥β;(3)
若m⊥α,m∥β,则α⊥β;(4)
若α∥β,且γ∩α=m,γ∩β=n,则m∥n.其中的正确命题是
[
]|
A .(1)和(3) |
B .(1)和(4) |
|
C .(2)和(4) |
D .(3)和(4) |
查看答案和解析>>
科目:高中数学 来源:2010-2011年四川省成都市高二3月月考数学试卷 题型:填空题
已知α,β是平面,m,n是直线. 给出下列命题:
①.若m∥n,m⊥α,则n⊥α ②.若m⊥α,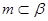 ,则α⊥β
,则α⊥β
③.若m⊥α,m⊥β,则α∥β ④.若m∥α,α∩β=n,则m∥n其中,真命题的编号是_ ▲ (写出所有正确结论的编号).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com