设函数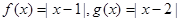 .
.
(1)解不等式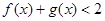 ;
;
(2)对于实数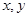 ,若
,若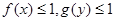 ,求证
,求证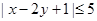 .
.
【答案】
(1)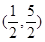 ;(2)见解析
;(2)见解析
【解析】本试题主要是考查了绝对值函数和绝对值不等式的求解的综合运用。
(1)利用已知函数令 ,则
,则
得到分段函数 的图像,研究其与直线y=2的交点即可
的图像,研究其与直线y=2的交点即可
(2)利用绝对值不等式的放缩来得到证明。
(1)解: (1)令 ,则
,则

作出函数 的图象,它与直线
的图象,它与直线 的交点为
的交点为 和
和

所以 的解集为
的解集为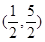 .
.
(2)因为

所以  .
.
练习册系列答案
相关习题
科目:高中数学
来源:庆安三中2010——2011学年度高二下学期期末考试数学(文)
题型:解答题
查看答案和解析>>
科目:高中数学
来源:2012届宁夏银川一中高三第一次月考理科数学试卷
题型:解答题
查看答案和解析>>
科目:高中数学
来源:2011-2012学年宁夏高三第一次月考文科数学试卷
题型:解答题
选修4—5:不等式选讲
设函数 .
.
(1)解不等式 ;
;
(2)求函数 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学
来源:2010-2011学年河南省高三上学期第一次月考理科数学卷
题型:解答题
(12分) 设函数 .
.
(1)解不等式 ;
;
(2)求函数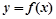 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学
来源:2010-2011学年宁夏高三第三次月考文科数学试卷
题型:解答题
选修4-5:不等式选讲
设函数 .
.
(1)解不等式 ;
;
(2)求函数 的最小值.
的最小值.
查看答案和解析>>

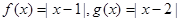 .
. 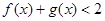 ;
;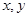 ,若
,若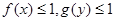 ,求证
,求证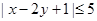 .
.