D
分析:采用换元法并结合二次函数的性质,算出当x∈[0,2]时,[f(x)]
min=-

,此时x=
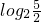
.然后类似地算出当x∈[-2,0]、x∈[-4,-2]、x∈[-6,-4]时,f(x)在各个区间上的最小值,即可得到若f(x)在[2n,2n+2]上的最小值为-
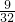
时,x∈[-6,-4],由此即可得到本题的答案.
解答:①∵当x∈[0,2]时,f(x)=
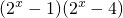
,
∴令2
x=t,得f(x)=(t-1)(t-4)=g(t)
当且仅当t=

时,[f(x)]
min=g(

)=-

,此时x=
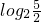
∈[0.2].
②当x∈[-2,0]时,f(x)=

f(x+2)=


,
类似①的方法,可得当x=
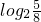
∈[-2,0)时,[f(x)]
min=-

;
③当x∈[-4,-2]时,f(x)=

f(x+2)=


类似①的方法,可得当x=
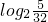
∈[-4,-2)时,[f(x)]
min=-

;
④当x∈[-6,-4]时,f(x)=

f(x+2)=

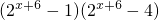
类似①的方法,可得当x=
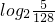
∈[-4,-2)时,[f(x)]
min=-
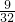
综上所述,若f(x)在[2n,2n+2]上的最小值为-
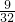
时,n=3
故选:D
点评:本题给出抽象函数f(x),在已知在x∈[0,2]时函数表达式且f(x+2)=2f(x)的情况下,求若f(x)在[2n,2n+2]上的最小值为-
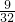
时n的值.着重考查了函数的对应法则、二次函数的图象与性质和函数值域求法等知识,属于中档题.

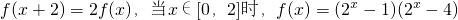 .若
.若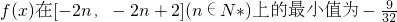 ,则n
,则n ,此时x=
,此时x=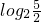 .然后类似地算出当x∈[-2,0]、x∈[-4,-2]、x∈[-6,-4]时,f(x)在各个区间上的最小值,即可得到若f(x)在[2n,2n+2]上的最小值为-
.然后类似地算出当x∈[-2,0]、x∈[-4,-2]、x∈[-6,-4]时,f(x)在各个区间上的最小值,即可得到若f(x)在[2n,2n+2]上的最小值为-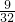 时,x∈[-6,-4],由此即可得到本题的答案.
时,x∈[-6,-4],由此即可得到本题的答案.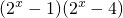 ,
, 时,[f(x)]min=g(
时,[f(x)]min=g( )=-
)=- ,此时x=
,此时x=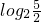 ∈[0.2].
∈[0.2]. f(x+2)=
f(x+2)=
 ,
,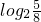 ∈[-2,0)时,[f(x)]min=-
∈[-2,0)时,[f(x)]min=- ;
; f(x+2)=
f(x+2)=

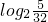 ∈[-4,-2)时,[f(x)]min=-
∈[-4,-2)时,[f(x)]min=- ;
; f(x+2)=
f(x+2)=
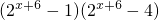
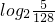 ∈[-4,-2)时,[f(x)]min=-
∈[-4,-2)时,[f(x)]min=-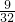
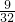 时,n=3
时,n=3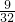 时n的值.着重考查了函数的对应法则、二次函数的图象与性质和函数值域求法等知识,属于中档题.
时n的值.着重考查了函数的对应法则、二次函数的图象与性质和函数值域求法等知识,属于中档题. 

 阅读快车系列答案
阅读快车系列答案