
分析 分离参数b,利用函数的单调性求出最值,最终求出b的范围.
解答 解:(1)①$-\frac{b}{2a}=-1,\frac{4ac-{b}^{2}}{4a}=0$
∴$;c=1,\\;a=1,b=2$a=1,b=2,
②∵(x+1)2>4,
∴x>1或x<-3.
(2)由题意知,函数f(x)=x2+bx,-1≤x2+bx≤1在区间(0,1]上恒成
即 b≤$\frac{1}{x}-x$且 $b≥-\frac{1}{x}-x$在(0,1]上恒成立.
根据单调性可得:$;y=\frac{1}{x}-x$ 的最小值为0,$;y=-\frac{1}{x}-x$ 的最大值为-2.
∴-2≤b≤0,
故b的取值范围为[-2,0].
点评 本题主要考查求函数的解析式,二次函数的性质应用,函数的恒成立问题,属于基础题.


 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案科目:高中数学 来源: 题型:解答题
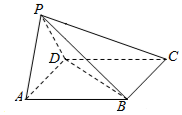 如图,在四棱锥P-ABCD中,平面PAD⊥平面ABCD,△PAD是等边三角形,四边形ABCD是平行四边形,∠ADC=120°,AB=2AD.
如图,在四棱锥P-ABCD中,平面PAD⊥平面ABCD,△PAD是等边三角形,四边形ABCD是平行四边形,∠ADC=120°,AB=2AD.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,四棱锥P-ABCD中,底面ABCD是梯形,AB∥CD,∠DAB=60°,AB=AD=2CD,侧面PAD⊥底面ABCD,且△PAD为等腰直角三角形,∠APD=90°,M为AP的中点.
如图,四棱锥P-ABCD中,底面ABCD是梯形,AB∥CD,∠DAB=60°,AB=AD=2CD,侧面PAD⊥底面ABCD,且△PAD为等腰直角三角形,∠APD=90°,M为AP的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
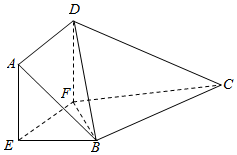 在直角梯形ABCD中,AB∥DC,AD⊥AB,DC=3,AB=2,AD=1,AE=EB,DF=1,现把它沿FE折起,得到如图所示几何体,连接DB,AB,DC,使DC=$\sqrt{5}$,
在直角梯形ABCD中,AB∥DC,AD⊥AB,DC=3,AB=2,AD=1,AE=EB,DF=1,现把它沿FE折起,得到如图所示几何体,连接DB,AB,DC,使DC=$\sqrt{5}$,查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com