
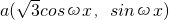 ,b(sinωx,0),且ω>0,设函数f(x)=(a+b)•b+k.
,b(sinωx,0),且ω>0,设函数f(x)=(a+b)•b+k. ,求ω的取值范围.
,求ω的取值范围.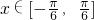 时,f(x)的最大值是2,求就k的值.
时,f(x)的最大值是2,求就k的值.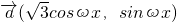 ,
, (sinωx,0),
(sinωx,0), +
+ =(
=( cosωx+sinωx,sinωx),
cosωx+sinωx,sinωx), sinωxcosωx+sin2ωx+k
sinωxcosωx+sin2ωx+k sin2ωx-
sin2ωx- cos2ωx+
cos2ωx+ +k
+k )+
)+ +k,
+k, =
= ,
, =
=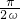 ≥
≥ ,∴ω≤1,又ω>0,
,∴ω≤1,又ω>0, =π,即ω=1,
=π,即ω=1, )+
)+ +k,
+k,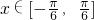 ,∴2x-
,∴2x- ∈[-
∈[- ,
, ],
], =
= ,即x=
,即x= 时,f(x)取得最大值,
时,f(x)取得最大值, )=2,及sin(2×
)=2,及sin(2× -
- )+
)+ +k=2,
+k=2, 和
和 的坐标求出
的坐标求出 +
+ 的坐标,进而利用平面向量的数量积运算法则算出(
的坐标,进而利用平面向量的数量积运算法则算出( +
+ )•
)• 的值,把f(x)的解析式变形,再利用二倍角的正弦、余弦函数公式化简,从而利用两角和与差的正弦函数公式及特殊角的三角函数值化为一个角的正弦函数,
的值,把f(x)的解析式变形,再利用二倍角的正弦、余弦函数公式化简,从而利用两角和与差的正弦函数公式及特殊角的三角函数值化为一个角的正弦函数, ,得到周期的一半大于等于
,得到周期的一半大于等于 ,再由ω>0即可求出ω的取值范围;
,再由ω>0即可求出ω的取值范围; 范围,根据正弦函数的图象与性质得到f(x)取得最大值时x的值,把求出x的值及f(x)的最大值为2代入f(x)解析式,即可求出k的值.
范围,根据正弦函数的图象与性质得到f(x)取得最大值时x的值,把求出x的值及f(x)的最大值为2代入f(x)解析式,即可求出k的值.

 作业辅导系列答案
作业辅导系列答案 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案科目:高中数学 来源:2011-2012学年第一学年度模块综合能力检测题(解析版) 题型:解答题
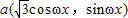 ,b(sinωx,0),且ω>0,设函数f(x)=(a+b)•b+k.
,b(sinωx,0),且ω>0,设函数f(x)=(a+b)•b+k.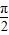 ,求ω的取值范围.
,求ω的取值范围.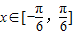 时,f(x)的最大值是2,求就k的值.
时,f(x)的最大值是2,求就k的值.查看答案和解析>>
科目:高中数学 来源:2009-2010学年北京市通州区高一(上)期末数学试卷(解析版) 题型:解答题
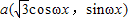 ,b(sinωx,0),且ω>0,设函数f(x)=(a+b)•b+k.
,b(sinωx,0),且ω>0,设函数f(x)=(a+b)•b+k. ,求ω的取值范围.
,求ω的取值范围.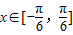 时,f(x)的最大值是2,求就k的值.
时,f(x)的最大值是2,求就k的值.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com