练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    在△ABC中，A=60°，C：b=8：5，内切圆的面积为12π，求△ABC的外接圆半径．

    解：设c=8k，则b=5k
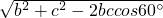
    由余弦定理可得a==7k
    ∴△ABC的面积=×5k×8k×sin60°=10k2
    由题意可知△ABC的内切圆的半径为2
    ∴10k2=×（8k+7k+5k）×2
    ∴k=2
    ∴a=14
    ∴外接圆的直径==
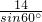
    ∴外接圆的半径径为
    分析：根据题意设出c，b，进而根据余弦定理表示出a，根据三角形面积公式求得三角形的面积的表达式，根据内切圆的面积求得出内切圆的半径，进而利用三边的长内切圆半径求得三角形的面积，联立等式求得k，则a可求，最后利用正弦定理求得三角形外接圆的直径，则半径可求．
    点评：本题主要考查了正弦定理和余弦定理的应用．考查了学生综合分析问题和基本的运算能力．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    在△ABC中，∠A=
    π
    6
    ，D是BC边上任意一点（D与B、C不重合），且丨
    AB
    |2=|
    AD
    |2+
    BD
    •
    DC
    ，则∠B=
     
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    在△ABC中，a=6，b=4，C=30°，则△ABC的面积是（　　）
    A、12
    B、6
    C、12
    		3
    D、8
    		3

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    在△ABC中，∠A=
    π
    6
    ，∠C=
    π
    2
    ，|AC|=
    		3
    ，M是AB的中点，那么(
    CA
    -
    CB
    )•
    CM
    =（　　）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    在△ABC中，∠A=
    π
    6
    ，D是BC边上任意一点（D与B，C不重合）且|
    AB
    |2=|
    AD
    |2+
    BD
    •
    DC
    ，则∠B    =（　　）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    在△ABC中，a=
    		6
    ，b=2，c=
    		3
    +1，求A、B、C及S△ABC．

    查看答案和解析>>

    同步练习册答案