

 x,得三棱锥P-ABC体积V=
x,得三棱锥P-ABC体积V= x2
x2 ,最后利用基本不等式求最值,可得当且仅当x=
,最后利用基本不等式求最值,可得当且仅当x= 时,正三棱锥P-ABC体积的最大值为
时,正三棱锥P-ABC体积的最大值为 .
.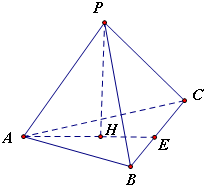 解:设H为底面△ABC的中心,延长AH交BC于E,连接PH
解:设H为底面△ABC的中心,延长AH交BC于E,连接PH AE=
AE=
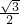 x=
x= x
x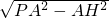 =
=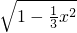
 S△ABC•AH=
S△ABC•AH= ×
× x2×
x2×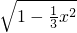
 x2
x2
 =2
=2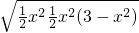 ,
, •
• •(3-x2)≤(
•(3-x2)≤(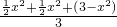 )3=1
)3=1 ≤2,可得V=
≤2,可得V= x2
x2 ≤
≤
 =3-x2时,即x=
=3-x2时,即x= 时,正三棱锥P-ABC体积的最大值为
时,正三棱锥P-ABC体积的最大值为



科目:高中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com