
点A(0,2)是圆x2+y2=16内的定点,点B,C是这个圆上的两个动点,若BA⊥CA,求BC中点M的轨迹方程,并说明它的轨迹是什么曲线。
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源:2013年湖北新洲、红安、麻城一中高三上学期期末考文科数学试卷(解析版) 题型:填空题
在平面直角坐标系xOy中,已知点A(0,2),直线l:x+y-4=0,点B(x,y)是圆C:x2+y2-2x-1=0上的动点,AD⊥l,BE⊥l,垂足分别为D、E,则线段DE的最大值是________.
查看答案和解析>>
科目:高中数学 来源:2010-2011学年辽宁省沈阳市四校协作体高三12月月考数学文卷 题型:解答题
(本小题满分12分)
已知定点A( ,0),B是圆C:(x-
,0),B是圆C:(x-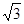 )2+y2=16,(C为圆心)上的动点,AB的垂直平分线与BC交与点E.
)2+y2=16,(C为圆心)上的动点,AB的垂直平分线与BC交与点E.
(1)求动点E的轨迹方程.
(2)设直线l:y=kx+m (k≠0,m>0)与E的轨迹交与P,Q两点,且以PQ为对角线的菱形的一顶点为M(-1,0),求△OPQ面积的最大值及此时直线l的方程.
查看答案和解析>>
科目:高中数学 来源:2011年高三数学单元检测:圆锥曲线(2)(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com