过原点与曲线y=x(x-1)(x-2)相切的直线方程是( )
A.2x-y=0
B.x+4y=0
C.2x-y=0或x+4y=0
D.2x-y=0或4x-y=0
【答案】
分析:先设切点坐标为P(a,b),然后根据导数的几何意义在x=a处的导数即为切线的斜率,以及切点曲线上,建立方程组,解之即可求出切点,再根据点斜时求出切线方程,最后化成一般式即可.
解答:解:设切点坐标为P(a,b),y'=3x
2-6x+2
则有

∴P(0,0)或(
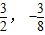
)
∴所求切线方程为2x-y=0或x+4y=0.
故选C.
点评:本题主要考查了导数的运算,以及利用导数研究曲线上某点切线方程问题,属于基础题.
