
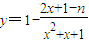 (n∈N*)的最小值为an,最大值为bn,又Cn=3(an+bn)-9
(n∈N*)的最小值为an,最大值为bn,又Cn=3(an+bn)-9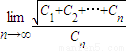 (n∈N*)的值
(n∈N*)的值 ,是否存在最小的整数m,使对任意的n∈N*都有
,是否存在最小的整数m,使对任意的n∈N*都有 成立?若存在,求出m的值;若不存在请说明理由.
成立?若存在,求出m的值;若不存在请说明理由. (n∈N*)的最小值为an,最大值为bn,从而可求数列{an}的通项公式;
(n∈N*)的最小值为an,最大值为bn,从而可求数列{an}的通项公式; ,从而Cn=4n-3 (n∈N*),求出Tn=C1+C2+…+Cn n(2n-1),即可求极限;
,从而Cn=4n-3 (n∈N*),求出Tn=C1+C2+…+Cn n(2n-1),即可求极限;
 ,从而数列{dn} 为递减数列,从而数列 {dn} 的最大项为
,从而数列{dn} 为递减数列,从而数列 {dn} 的最大项为 ,
, 恒成立,只需
恒成立,只需 ,故可求最小的整数.
,故可求最小的整数.
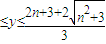
 (n∈N*)的最小值为an,最大值为bn
(n∈N*)的最小值为an,最大值为bn
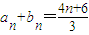 于是Cn=4n-3 (n∈N*) …4分
于是Cn=4n-3 (n∈N*) …4分
 =
=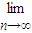
 …8分
…8分

 ,
, 恒成立,只需
恒成立,只需 ,
, ,故最小的整数m=8.…13分
,故最小的整数m=8.…13分

 金钥匙试卷系列答案
金钥匙试卷系列答案科目:高中数学 来源: 题型:
| 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| a+1 | x |
查看答案和解析>>
科目:高中数学 来源:杭州一模 题型:解答题
| 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:
(1)求证:an+1 +an-1<![]() aN(N=1,2…).
aN(N=1,2…).
(2)设bN=an+1-2aN,N=0,1,2,….求证: bN<(-6)(![]() )n(N∈N*).
)n(N∈N*).
(3)是否存在常数A和B,同时满足:
①当N=0及N=1时,有an=![]() 成立;
成立;
②当N=2,3…时,有an<![]() 成立.
成立.
如果存在满足上述条件的实数A、B,求出A、B的值;如果不存在,证明你的结论.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com