分析:由题设△A
k-1B
kA
k(k=1,2,…)都是等边三角形,设第n个等边三角形的边长为a
n.则可得出第n个等边三角形的在抛物线上的顶点B
n的坐标为(
a1+a2+…+an-1+,
).再在第n个正三角形中求出它的高即可得到点B
n的纵坐标的另一种表示为
=an.由此得到恒等式
an=,利用此恒等式即可解出a
n=n,从而得到第2011个等边三角形的边长.
解答:解:(1)设第n个等边三角形的边长为a
n.则第n个等边三角形的在抛物线上的顶点B
n的坐标为(
a1+a2+…+an-1+,
).
再从第n个等边三角形中,可得B
n的纵坐标为
=an.
从而有
an=,
即有
=a1+a2+…+an-1+.
由此可得
a1+a2+…+an=+①
以及
a1+a2+…+an-1=+②
①-②即得
an=(an-an-1)+(an-an-1)(an+an-1).
变形可得(a
n-a
n-1-1)(a
n+a
n-1)=0.
由于a
n+a
n-1≠0,所以a
n-a
n-1=1.
在①式中取n=1,可得
a1=,而a
1≠0,故a
1=1.所以a
n=n
∴第2011个等边三角形的边长 a
2011=2011
故答案为2011
点评:本题考查数列与解析几何的综合,本题有一定的探究性,解题的关键是将点Bn的纵坐标用两种形式表示出来从而得出恒成立的等式,本题综合性强运算量大,解题时要严谨答题避免马虎出错导致解题失败.本题考查了数形结合的技巧及转化的思想,是高考中的易考题型



 上从左向右依次取点列{Bk},k=1,2,…,使△Ak-1BkAk(k=1,2,…)都是等边三角形,其中A是坐标原点,则第2011个等边三角形的边长是 .
上从左向右依次取点列{Bk},k=1,2,…,使△Ak-1BkAk(k=1,2,…)都是等边三角形,其中A是坐标原点,则第2011个等边三角形的边长是 .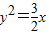 上从左向右依次取点列Bk,k=1,2,…,使△Ak-1BkAk(k=1,2,…)都是等边三角形,其中A是坐标原点,设第n个等边三角形的边长为an.
上从左向右依次取点列Bk,k=1,2,…,使△Ak-1BkAk(k=1,2,…)都是等边三角形,其中A是坐标原点,设第n个等边三角形的边长为an.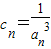 ,求证:
,求证: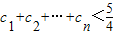 .
.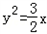 上从左向右依次取点列{Bk},k=1,2,…,使△Ak﹣1BkAk(k=1,2,…)都是等边三角形,其中A0是坐标原点,则第2011个等边三角形的边长是( )。
上从左向右依次取点列{Bk},k=1,2,…,使△Ak﹣1BkAk(k=1,2,…)都是等边三角形,其中A0是坐标原点,则第2011个等边三角形的边长是( )。