练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    已知函f(x)＝ax3＋x2＋bx(其中常数a，b∈R)，g(x)＝f(x)＋是奇函数．

    (1)求f(x)的表达式；

    (2)试论g(x)的单调性，并求g(x)在区间[1，2]上的最大值与最小值．

    答案：利用函数的奇偶性来求参数
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：随堂练1＋2　讲·练·测　高中数学·必修1（苏教版） 苏教版 题型：044

    已知f(x)＝ax(a＞0且a≠1)在[－2，2]上，函数值总小于2．求实数a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源：新课程高中数学疑难全解 题型：044

    已知y＝f(x)＝x2＋ax＋b，设x＝1时函数值为y1，即y1＝f(x1)，x＝2时，函数值为y2＝f(x2)，x＝3时的函数值为y3＝f(x3)．

    (1)求y1－2y2＋y3的值；

    (2)求证：|y1|，|y2|，|y3|中至少有一个不小于

    查看答案和解析>>

    科目：高中数学 来源：内蒙古赤峰二中2010－2011学年高二下学期期末考试数学文科试题 题型：013

    已知函数f(x)＝(x－a)(x－b)(其中a＞b)的图象如下图所示，则函g(x)＝ax＋b的图象是

    [　　]

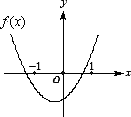
    A．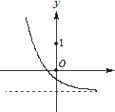

    B．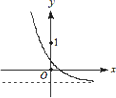

    C．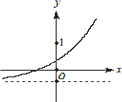

    D．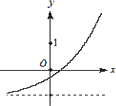

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知函数f(x)＝loga(ax－1)(a>0且a≠1)

    (1)求f(x)的定义域；

    (2)讨论f(x)的单调性；

    (3)x为何值时，函数值大于1.

    查看答案和解析>>

    同步练习册答案