
分析 由新定义,结合圆的参数方程可得x=2cosα,y=2sinα(0≤α<2π),通过举例即可判断①不对,②正确;
再由同角的平方关系,举例判断③不正确;对于④,通过推理,假设存在这样的有理点,即可得到不成立.
解答 解:由x2+y2=4,可设x=2cosα,y=2sinα(0≤α<2π),
可得点(0,2),(0,-2),(-2,0),(2,0),($\frac{6}{5}$,$\frac{8}{5}$),($\frac{6}{5}$,-$\frac{8}{5}$),
(-$\frac{6}{5}$,$\frac{8}{5}$),(-$\frac{6}{5}$,-$\frac{8}{5}$),($\frac{8}{5}$,$\frac{6}{5}$),($\frac{8}{5}$,-$\frac{6}{5}$),(-$\frac{8}{5}$,$\frac{6}{5}$),(-$\frac{8}{5}$,-$\frac{6}{5}$),…,满足条件,
故①不对,②正确;
对于③,由x2+y2=4,可得($\sqrt{2}$,$\sqrt{2}$),($\sqrt{2}$,-$\sqrt{2}$),(-$\sqrt{2}$,$\sqrt{2}$),(-$\sqrt{2}$,-$\sqrt{2}$),
($\sqrt{1.1}$,$\sqrt{2.9}$),…,均满足条件,
故③不正确;
对于④,⊙O上点(1,$\sqrt{3}$)为圆心,半径为4的圆,
可设为(x-1)2+(y-$\sqrt{3}$)2=16,若x,y均为有理数,则y必为0,x不为有理数,
故不存在这样的有理点.故④错误.
故答案为:②.
点评 本题考查新定义的理解和运用,考查圆的方程的运用,考查推理能力,属于中档题.


科目:高中数学 来源: 题型:解答题
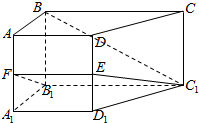 如图所示,在侧棱垂直于底面的四棱柱ABCD-A1B1C1D1中,AD∥BC,AD⊥AB,AB=$\sqrt{2}$,AD=2,BC=4,AA1=2,E、F分别是DD1,AA1的中点.
如图所示,在侧棱垂直于底面的四棱柱ABCD-A1B1C1D1中,AD∥BC,AD⊥AB,AB=$\sqrt{2}$,AD=2,BC=4,AA1=2,E、F分别是DD1,AA1的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {2,3} | B. | {0,1,2} | C. | {1,2,3} | D. | {0,1} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
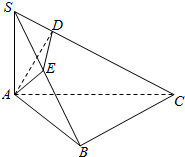 如图,在三棱锥S-ABC中,∠ABC=90°,SA⊥平面ABC,点A在SB和SC上的射影分别为E、D.
如图,在三棱锥S-ABC中,∠ABC=90°,SA⊥平面ABC,点A在SB和SC上的射影分别为E、D.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 25π | B. | 32π | C. | 36π | D. | 50π |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com