解:(Ⅰ)因为
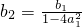
=

,所以a
2=a
1b
2=

.所以P
2(

,

).
所以过点P
1,P
2的直线l的方程为 2x+y=1.
(Ⅱ)∵已知点P
n(a
n,b
n)(n∈N)在P
1,P
2两点确定的直线l上,
∴2a
n+b
n=1.
由a
n+1=a
nb
n+1 可得 a
n+1=a
n(1-2a
n+1),
∴

=
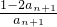
,即

-

=2,故{

}是公差等于2的等差数列.
所以

=1+2(n-1)=2n-1,所以a
n=

.
(Ⅲ)由上可得 b
n=1-2a
n=

.依题意 k≤(1+a
1)(1+a
2)(1+a
3)…(1+a
n)
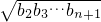
恒成立.
设F(n)=(1+a
1)(1+a
2)(1+a
3)…(1+a
n)
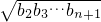
,所以只需求满足 k≤F(n)的F(n)的最小值.
∵

=
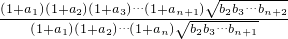
=(1+a
n+1)
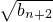
=
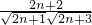
=
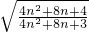
>1,
所以F(n) (x∈N
*)为增函数.
所以F(n)
min=F(1)=

=

.
所以 k≤

.
所以k
max=

.
分析:(Ⅰ)先求出a
2 和b
2 的值,即可得到P
2 的坐标,用两点式求得过点P
1,P
2的直线l的方程.
(Ⅱ)把已知点P
n的坐标代入直线l的方程可得 2a
n+b
n=1,化简可得

-

=2,故{

}是公差等于2的等差数列,由此求得数列{a
n}通项公式.
(Ⅲ)由上可得 b
n=1-2a
n=

.依题意 k≤(1+a
1)(1+a
2)(1+a
3)…(1+a
n)
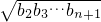
恒成立.设F(n)=(1+a
1)(1+a
2)(1+a
3)…(1+a
n)
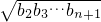
,利用单调性求得F(n)
min=F(1),故 k≤F(1),运算求得结果.
点评:本题主要考查等差关系的确定,数列与不等式的综合,数列的函数特性,函数的恒成立问题,属于难题.

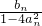 ,且点P1的坐标为(1,-1).
,且点P1的坐标为(1,-1).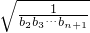 成立的最大实数k的值.
成立的最大实数k的值.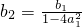 =
= ,所以a2=a1b2=
,所以a2=a1b2= .所以P2(
.所以P2(  ,
, ).
). =
=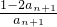 ,即
,即 -
- =2,故{
=2,故{ }是公差等于2的等差数列.
}是公差等于2的等差数列. =1+2(n-1)=2n-1,所以an=
=1+2(n-1)=2n-1,所以an= .
. .依题意 k≤(1+a1)(1+a2)(1+a3)…(1+an)
.依题意 k≤(1+a1)(1+a2)(1+a3)…(1+an)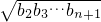 恒成立.
恒成立.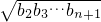 ,所以只需求满足 k≤F(n)的F(n)的最小值.
,所以只需求满足 k≤F(n)的F(n)的最小值. =
=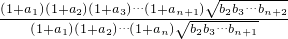 =(1+an+1)
=(1+an+1)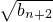 =
=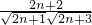 =
=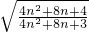 >1,
>1, =
= .
. .
. .
. -
- =2,故{
=2,故{ }是公差等于2的等差数列,由此求得数列{an}通项公式.
}是公差等于2的等差数列,由此求得数列{an}通项公式. .依题意 k≤(1+a1)(1+a2)(1+a3)…(1+an)
.依题意 k≤(1+a1)(1+a2)(1+a3)…(1+an)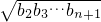 恒成立.设F(n)=(1+a1)(1+a2)(1+a3)…(1+an)
恒成立.设F(n)=(1+a1)(1+a2)(1+a3)…(1+an)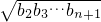 ,利用单调性求得F(n)min=F(1),故 k≤F(1),运算求得结果.
,利用单调性求得F(n)min=F(1),故 k≤F(1),运算求得结果.

 作业辅导系列答案
作业辅导系列答案 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案