
已知曲线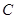 :
: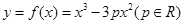 .
.
(Ⅰ)当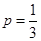 时,求曲线
时,求曲线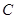 的斜率为1的切线方程;
的斜率为1的切线方程;
(Ⅱ)设斜率为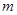 的两条直线与曲线
的两条直线与曲线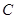 相切于
相切于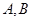 两点,求证:
两点,求证: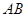 中点
中点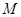 在曲线
在曲线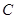 上;
上;
(Ⅲ)在(Ⅱ)的条件下,又已知直线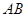 的方程为:
的方程为: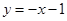 ,求
,求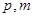 的值.
的值.
(Ⅰ)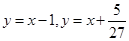 ;(Ⅱ)详见解析;(Ⅲ)
;(Ⅱ)详见解析;(Ⅲ)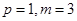 .
.
【解析】
试题分析:(Ⅰ)当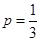 时,先求导,通过斜率为1得到切点.然后利用点斜式得到所求切线方程;(Ⅱ)先将
时,先求导,通过斜率为1得到切点.然后利用点斜式得到所求切线方程;(Ⅱ)先将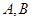 两点的坐标设出,其中纵坐标用相应点的横坐标表示.再由导数的几何意义,得到
两点的坐标设出,其中纵坐标用相应点的横坐标表示.再由导数的几何意义,得到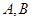 两点横坐标满足
两点横坐标满足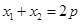 .从而得到
.从而得到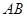 中点
中点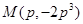 ,又
,又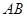 中点
中点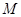 在曲线
在曲线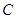 上
上 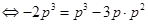 ,显然成立.得证;(Ⅲ)由
,显然成立.得证;(Ⅲ)由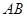 中点在直线
中点在直线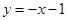 ,又在曲线
,又在曲线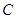 ,从而得
,从而得 ,再反代如直线与曲线联立得方程,得到
,再反代如直线与曲线联立得方程,得到 两点的坐标,代入导函数中得到斜率,从而得到
两点的坐标,代入导函数中得到斜率,从而得到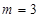 .
.
试题解析:(Ⅰ)当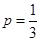 时,
时,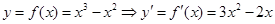 ,
,
设切点为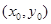 ,由
,由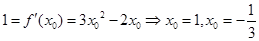 ,切点为
,切点为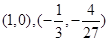
故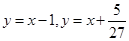 为所求.
(4分)
为所求.
(4分)
(Ⅱ)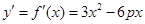 ,设
,设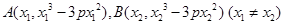 ,
,
由导数的几何意义有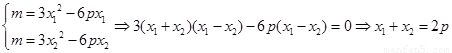

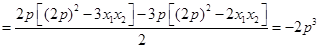
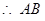 中点
中点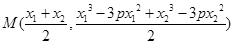 ,即
,即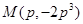 ,
,
又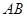 中点
中点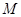 在曲线
在曲线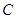 上
上 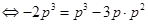 ,显然成立.得证.
(8分)
,显然成立.得证.
(8分)
(Ⅲ)由(Ⅱ)知,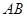 中点
中点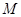 的横坐标为
的横坐标为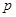 ,且
,且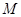 在
在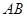 上,
上,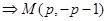 ,
,
又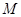 在曲线
在曲线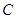 上,
上,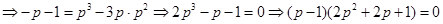 ,
,
所以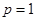 .
.
由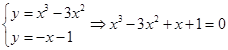 ,
,
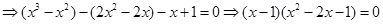
由于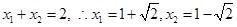 ,
,
故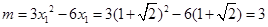 .
.
综上,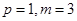 为所求.
(13分)
为所求.
(13分)
考点:1.导数的几何意义;2.直线的方程;3.直线与曲线的位置关系.


 高效智能课时作业系列答案
高效智能课时作业系列答案 捷径训练检测卷系列答案
捷径训练检测卷系列答案科目:高中数学 来源: 题型:
| AP |
| PB |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 (坐标系与参数方程选做题).
(坐标系与参数方程选做题).
|
查看答案和解析>>
科目:高中数学 来源: 题型:
|
|
| MF2+DM2 |
| 302+1702 |
| 198 |
查看答案和解析>>
科目:高中数学 来源: 题型:
|
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| x |
|
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com