
【题目】如图,关于正方体ABCD﹣A1B1C1D1 , 下面结论错误的是( ) 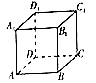
A.BD⊥平面ACC1A1
B.AC⊥BD
C.A1B∥平面CDD1C1
D.该正方体的外接球和内接球的半径之比为2:1
【答案】D
【解析】解:由正方体ABCD﹣A1B1C1D1,知:
在A中,∵BD⊥AC,BD⊥AA1,AC∩AA1=A,∴BD⊥平面ACC1A1,故A正确;
在B中,∵ABCD是正方形,∴AC⊥BD,故B正确;
在C中,∵A1B∥D1C,A1B平面CDD1C1,D1C平面CDD1C1,故A1B∥平面CDD1C1,故C正确;
在D中,该正方体的外接球和内接球的半径之比为 ![]() =
= ![]() :1.故D错误.
:1.故D错误.
故选:D.
【考点精析】根据题目的已知条件,利用棱柱的结构特征的相关知识可以得到问题的答案,需要掌握两底面是对应边平行的全等多边形;侧面、对角面都是平行四边形;侧棱平行且相等;平行于底面的截面是与底面全等的多边形.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】如图,在正方体ABCD﹣A1B1C1D1中,AB=2,点E是BC的中点. 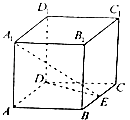
(1)求线段DE的长;
(2)求直线A1E与平面ADD1A1所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆C:x2+y2﹣2x+4y﹣4=0,是否存在斜率为1的直线l,使l被圆C截得的弦长AB为直径的圆过原点,若存在求出直线的方程l,若不存在说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知甲、乙两名同学在某项测试中得分成绩的茎叶图如图所示,x1 , x2分别表示知甲、乙两名同学这项测试成绩的众数,s12 , s22分别表示知甲、乙两名同学这项测试成绩的方差,则有( ) 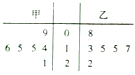
A.x1>x2 , s12<s22
B.x1=x2 , s12>s22
C.x1=x2 , s12=s22
D.x1=x2 , s12<s22
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知a∈R,当x>0时,f(x)=log2( ![]() +a).
+a).
(1)若函数f(x)过点(1,1),求此时函数f(x)的解析式;
(2)若函数g(x)=f(x)+2log2x只有一个零点,求实数a的范围;
(3)设a>0,若对任意实数t∈[ ![]() ,1],函数f(x)在[t,t+1]上的最大值与最小值的差不大于1,求实数a的取值范围.
,1],函数f(x)在[t,t+1]上的最大值与最小值的差不大于1,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知:θ为第一象限角, ![]() =(sin(θ﹣π),1),
=(sin(θ﹣π),1), ![]() =(sin(
=(sin( ![]() ﹣θ),﹣
﹣θ),﹣ ![]() ),
),
(1)若 ![]() ∥
∥ ![]() ,求
,求 ![]() 的值;
的值;
(2)若| ![]() +
+ ![]() |=1,求sinθ+cosθ的值.
|=1,求sinθ+cosθ的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com