
【题目】某地建一座桥,两端的桥墩已建好,这两墩相距m米,余下的工程只需要建两端桥墩之间的桥面和桥墩.经预测一个桥墩的工程费用为256万元,距离为x米的相邻两墩之间的桥面工程费用为(2+ ![]() )x万元.假设桥墩等距离分布,所有桥墩都视为点,且不考虑其他因素,记余下工程的费用为y万元.假设需要新建n个桥墩.
)x万元.假设桥墩等距离分布,所有桥墩都视为点,且不考虑其他因素,记余下工程的费用为y万元.假设需要新建n个桥墩.
(1)写出n关于x的函数关系式;
(2)写出y关于x的函数关系式;
(3)当m=640米时,需新建多少个桥墩才能使y最小?
【答案】
(1)解: ![]()
(2)解:∴ ![]()
= ![]()
(3)解:由(1)知, 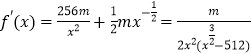
令f'(x)=0,得 ![]() ,所以x=64
,所以x=64
当0<x<64时f'(x)<0,f(x)在区间(0,64)内为减函数;
当64<x<640时,f'(x)>0,f(x)在区间(64,640)内为增函数,
所以f(x)在x=64处取得最小值,
此时, ![]()
故需新建9个桥墩才能使y最小
【解析】(1)利用两墩相距m米,写出n关于x的函数关系式;(2)根据题意余下工程的费用y为桥墩的总费用加上相邻两墩之间的桥面工程总费用即可得到y的解析式;(3)把m=640米代入到y的解析式中并求出y′令其等于0,然后讨论函数的增减性判断函数的最小值时m的值代入 ![]() ﹣1中求出桥墩个数即可.
﹣1中求出桥墩个数即可.


 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() +3lnax﹣x,g(x)=xex+cosx(a≠0).
+3lnax﹣x,g(x)=xex+cosx(a≠0).
(1)求函数y=f(x)的单调区间;
(2)若x1∈[1,2],x2∈[0,3],使得f( ![]() )>g(x2)成立,求实数a的取值范围.
)>g(x2)成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
已知曲线![]() 的极坐标方程为
的极坐标方程为![]() ,以极点为平面直角坐标系的原点,极轴为
,以极点为平面直角坐标系的原点,极轴为![]() 的正半轴,建立平面直角坐标系
的正半轴,建立平面直角坐标系![]() .
.
(1)若曲线![]() 为参数)与曲线
为参数)与曲线![]() 相交于两点
相交于两点![]() ,求
,求![]() ;
;
(2)若![]() 是曲线
是曲线![]() 上的动点,且点
上的动点,且点![]() 的直角坐标为
的直角坐标为![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知 ![]() =(sinx,cosx),
=(sinx,cosx), ![]() =(sinx,sinx),函数f(x)=
=(sinx,sinx),函数f(x)= ![]() .
.
(1)求f(x)的对称轴方程;
(2)求使f(x)≥1成立的x的取值集合;
(3)若对任意实数 ![]() ,不等式f(x)﹣m<2恒成立,求实数m的取值范围.
,不等式f(x)﹣m<2恒成立,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有能力互异的3人应聘同一公司,他们按照报名顺序依次接受面试,经理决定“不录用第一个接受面试的人,如果第二个接受面试的人比第一个能力强,就录用第二个人,否则就录用第三个人”,记该公司录用到能力最强的人的概率为p,录用到能力中等的人的概率为q,则(p,q)=( )
A.( ![]() ,
, ![]() )
)
B.( ![]() ,
, ![]() )
)
C.( ![]() ,
, ![]() )
)
D.( ![]() ,
, ![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义域为R的函数f(x)= ![]() 是奇函数.
是奇函数.
(Ⅰ)求b的值;
(Ⅱ)判断函数f(x)的单调性;
(Ⅲ)若对任意的t∈R,不等式f(t2﹣2t)+f(2t2﹣k)<0恒成立,求k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() :
:![]() ,
,![]() ,
,![]() 是圆
是圆![]() 上的一个动点,线段
上的一个动点,线段![]() 的垂直平分线与线段
的垂直平分线与线段![]() 相交于点
相交于点![]() .
.
(Ⅰ)求点![]() 的轨迹方程;
的轨迹方程;
(Ⅱ)记点![]() 的轨迹为
的轨迹为![]() ,
,![]() ,
,![]() 是直线
是直线![]() 上的两点,满足
上的两点,满足![]() ,曲线
,曲线![]() 的过
的过![]() ,
,![]() 的两条切线(异于
的两条切线(异于![]() )交于点
)交于点![]() ,求四边形
,求四边形![]() 面积的取值范围.
面积的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com